Classical vs Bayesian Methods for Sensor Reliability Analysis: A Comprehensive Guide for Biomedical Researchers

Abstract

This article provides a systematic comparison of classical and Bayesian statistical methods for analyzing sensor reliability in biomedical and drug development applications. It covers foundational principles, from the frequentist interpretation of probability to Bayesian prior incorporation, and details methodological applications for success/no-success data and complex system modeling. The guide addresses common challenges like limited failure data and uncertainty quantification, offering optimization strategies such as hierarchical Bayesian models. Through validation frameworks and case studies, including wearables and reliability testing, it demonstrates the comparative advantages of each approach. Aimed at researchers and professionals, this review synthesizes key takeaways to inform robust sensor reliability practices in clinical research and therapeutic development.

Understanding the Core Principles: Frequency vs. Belief in Probability

In statistical analysis, the interpretation of probability itself is not a monolith but branches into two primary schools of thought: the classical frequency-based and the Bayesian belief-based paradigms. This distinction is not merely academic; it forms the foundational bedrock upon which statistical inference is built, influencing everything from experimental design in scientific research to decision-making in industrial reliability engineering. The classical, or frequentist, approach interprets probability as the long-run frequency of an event occurring in repeated, identical trials. In contrast, the Bayesian approach treats probability as a subjective measure of belief or uncertainty about an event, which can be updated as new evidence emerges [1] [2] [3]. Within the specific context of sensor reliability and degradation analysis—where data may be scarce, costly to obtain, or heavily censored—the choice between these paradigms dictates how parameters are estimated, risks are quantified, and maintenance strategies are ultimately formulated [4] [5]. This guide provides a structured, objective comparison of these two philosophical foundations, equipping researchers and engineers with the knowledge to select the appropriate tool for their specific reliability challenge.

Core Philosophical Divergence

The most fundamental difference between the classical and Bayesian paradigms lies in their very definition of probability. This philosophical schism leads to profoundly different approaches to statistical analysis and inference.

• Classical (Frequentist) Probability: In this framework, probability is strictly defined as the limit of a relative frequency over a long series of repeated trials [2]. For example, a frequentist would state that the probability of a fair coin landing on heads is 0.5 because, in a vast number of tosses, the relative frequency of heads converges to 50%. This interpretation is objective; it is considered a property of the real world. Consequently, parameters of a system, such as the mean time to failure of a sensor, are treated as fixed, unknown constants. It does not make mathematical sense to assign a probability distribution to a fixed parameter [2] [3]. Statistical conclusions are based solely on the data observed in the current sample, and inferences are framed in terms of the long-run behavior of estimators and tests.

• Bayesian Probability: Bayesian statistics interprets probability as a subjective degree of belief in a proposition or the state of the world [6] [3]. This belief is quantified on a scale from 0 to 1 and is personal, as it depends on the prior knowledge of the individual assessing the probability. This view allows for the assignment of probabilities to one-off events where long-run frequencies are meaningless. For instance, a Bayesian can assign a probability to the statement, "This specific sensor will function for more than 10,000 hours," based on available knowledge [7] [2]. In this framework, all unknown quantities, including parameters, are treated as random variables with probability distributions that represent our uncertainty about their true values. This belief is updated logically and mathematically as new data becomes available via Bayes' theorem.

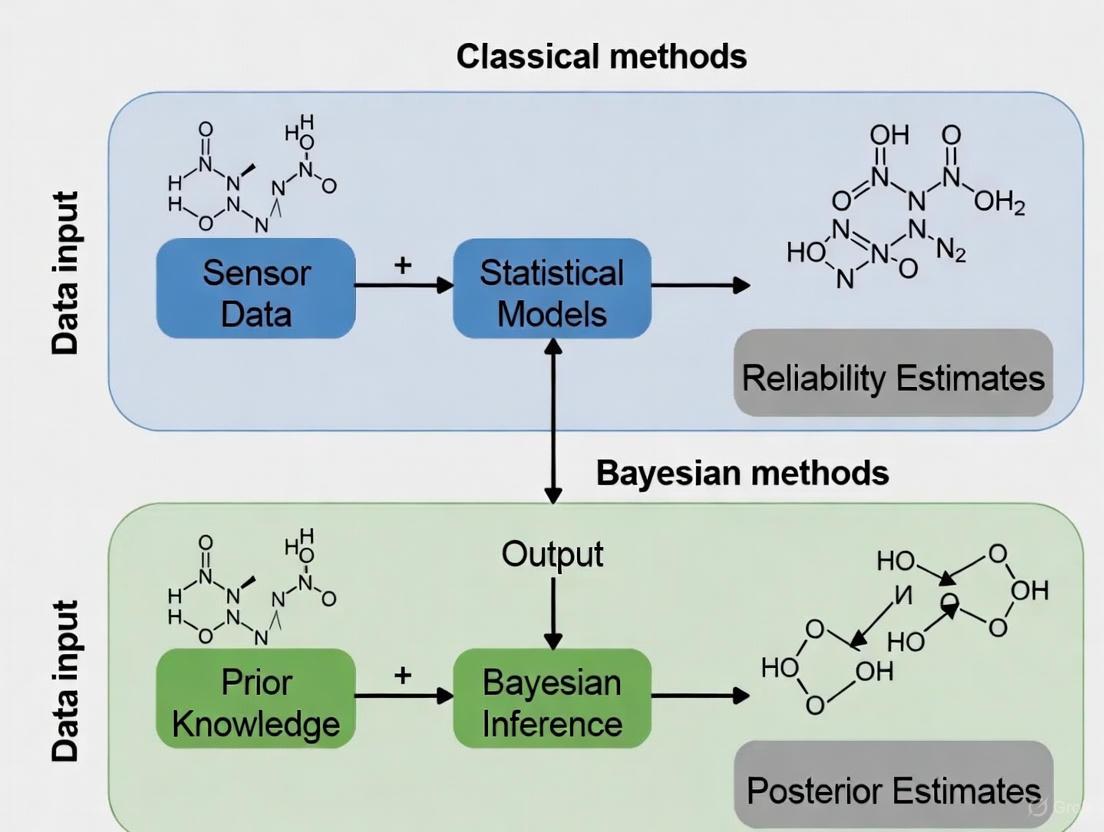
The following conceptual diagram illustrates the fundamental difference in how these two paradigms process information to reach a statistical conclusion.

Methodological Comparison and Experimental Protocols

The philosophical divergence translates into distinct methodologies for conducting analysis. The core of the Bayesian methodology is a mathematical framework for updating beliefs, while the frequentist method relies on comparing observed data to a sampling distribution.

The Bayesian Update Mechanism

At the heart of Bayesian statistics is Bayes' Theorem, which provides a formal mechanism for updating prior beliefs in light of new evidence [1] [6]. The formula is:

Posterior ∝ Likelihood × Prior

Or, more formally: π(θ | x) = [ p(x | θ) * π(θ) ] / p(x)

Where:

• Ï€(θ | x) is the posterior distribution: the updated belief about the parameter θ after observing the data x.
• p(x | θ) is the likelihood function: the probability of observing the data x given a specific value of θ.
• Ï€(θ) is the prior distribution: the belief about θ before observing the data x.
• p(x) is the marginal likelihood: a normalizing constant that ensures the posterior distribution is a valid probability distribution [6].

This process is iterative. The posterior distribution from one analysis can serve as the prior for the next update when new data is collected, creating a continuous learning cycle [1] [8].

Frequentist Hypothesis Testing Protocol

Frequentist methodology revolves around a structured procedure of null hypothesis significance testing (NHST). A typical experimental protocol is as follows [8] [9]:

• Define Hypotheses: Formulate a null hypothesis (Hâ‚€), often representing "no effect" (e.g., two sensor types have the same mean time to failure), and an alternative hypothesis (H₁).
• Choose Test Statistic: Select a statistic (e.g., t-statistic, F-statistic) that measures the evidence against Hâ‚€.
• Collect Data: Conduct an experiment or collect a sample.
• Calculate p-value: Compute the probability of observing a test statistic as extreme as, or more extreme than, the one calculated from the sample, assuming the null hypothesis is true.
• Make Decision: Reject or fail to reject Hâ‚€ by comparing the p-value to a pre-specified significance level (α, typically 0.05). This decision is based on the concept of "what if the experiment were repeated infinitely?" rather than the probability of the hypothesis itself [2] [9].

Side-by-Side Comparison of Key Elements

The table below summarizes the core components of both approaches for direct comparison.

Element	Classical (Frequentist) Approach	Bayesian Approach
Probability Interpretation	Objective long-run frequency [2] [3]	Subjective degree of belief or uncertainty [6] [3]
Parameter Treatment	Fixed, unknown constants [2]	Random variables with probability distributions [2] [9]
Prior Information	Not incorporated formally into analysis [9]	Incorporated explicitly via the prior distribution [1] [6]
Primary Output	Point estimates (e.g., MLE), Confidence Intervals (CI), p-values [8] [3]	Full posterior distribution, Credible Intervals [1] [2]
Result Interpretation	A 95% CI means that in repeated sampling, 95% of such intervals will contain the true parameter [2].	A 95% Credible Interval means there is a 95% probability the parameter lies within this interval, given the data [2].
Handling Uncertainty	Uncertainty is quantified through the sampling distribution of the estimator [3].	Uncertainty is quantified directly through the posterior distribution of the parameter [3].

Application in Sensor Reliability and Degradation Analysis

In reliability engineering, particularly for critical components like sensor systems, both paradigms offer tools for analyzing failure and degradation data, often under constraints like Type II censoring where a test is terminated after a pre-set number of failures [4].

Classical Reliability Methods

The classical approach to reliability, such as designing a failure-censored sampling plan for a lognormal lifetime model, involves calculating producer's and consumer's risks based solely on the observed failure data and the assumed distribution [4]. These methods use tools like:

• Accelerated Life Tests (ALT) and Design of Experiments (DOE) to understand how factors affect performance and predict failure distributions [5].
• Operating Characteristic (OC) Curves to evaluate the probability of accepting a batch given its quality level [4].

A key limitation is that when no failures occur during testing, classical methods struggle to quantify the probability of failure with precision, as they rely exclusively on the observed (zero) failure count [6].

Bayesian Reliability Methods

Bayesian methods are particularly powerful in reliability analysis due to their ability to incorporate prior knowledge—such as expert opinion, historical data, or simulation results—which is invaluable when failure data is scarce or expensive to obtain [6] [5].

• Incorporating Expert Opinion: A prior distribution for a sensor's reliability can be defined using a Beta distribution, which is flexible and conjugate to the binomial likelihood for success/failure data [6]. The parameters α and β can be chosen so that the prior's mean reflects the expert's belief about the reliability, and its variance reflects their confidence in that belief.
• Handling Zero-Failure Tests: Even if a new test yields zero failures, the Bayesian posterior distribution will be a blend of the prior and the new data. This allows for a quantitative estimate of reliability that is more informative than a classical estimate based on zero failures alone [6].
• Complex System Reliability: For a system composed of multiple subcomponents, a Bayesian approach combined with Monte Carlo algorithms can compute the posterior distribution of the entire system's reliability, even when only system-level test data is available [6].

The workflow below illustrates how a reliability engineer might apply the Bayesian approach to a component degradation problem, integrating multiple data sources.

Comparative Performance in a Case Study

A study on locomotive wheel-sets, a critical sensor-rich subsystem, compared classical and Bayesian semi-parametric degradation approaches for optimizing preventive maintenance. The study found that both approaches were useful tools for analyzing degradation data and supporting maintenance decisions. Notably, it concluded that the results from the different models can be complementary, providing a more robust foundation for decision-making [5]. The Bayesian approach, with its ability to model group-level effects (e.g., different bogies) through "frailties," offered a way to account for unobserved covariates that could influence degradation, a flexibility not as readily available in standard classical methods [5].

The Researcher's Toolkit: Essential Analytical Components

When implementing the methodologies discussed, researchers rely on a set of conceptual and software-based "reagents" to conduct their analysis.

Conceptual Components for Reliability Analysis

Component	Function	Frequentist Example	Bayesian Example
Probability Model	Describes the random process generating the data.	Lognormal failure time distribution [4].	Lognormal failure time with a prior on its parameters [4].
Estimation Method	The algorithm or formula for deriving parameter values.	Maximum Likelihood Estimation (MLE).	Markov Chain Monte Carlo (MCMC) for posterior sampling [10] [9].
Interval Estimate	Quantifies uncertainty about a parameter's value.	95% Confidence Interval [4].	95% Credible Interval (Bayesian counterpart) [4].
Risk Function	Evaluates the cost of incorrect decisions in sampling plans.	Producer’s and Consumer’s risk [4].	Average and Posterior risks, which incorporate prior belief [4].
Azadiradione	Azadiradione Research Compound|Neem-Derived Limonoid		Bench Chemicals
20-Deoxocarnosol	20-Deoxocarnosol, MF:C20H28O3, MW:316.4 g/mol	Chemical Reagent	Bench Chemicals

Software and Computational Tools

The practical application of these methods is enabled by statistical software and libraries.

• R: For frequentist analysis, R has extensive built-in functions and packages for survival analysis (survival package) and reliability. For Bayesian analysis, packages like rstan, brms, and bayesAB provide powerful MCMC sampling capabilities [9].
• Python: The scipy.stats and lifelines libraries support classical reliability and survival analysis. For Bayesian modeling, pymc3 (now pymc) and stan (via pystan) are industry standards [9].
• SAS: Procedures like PROC LIFEREG (classical) and PROC MCMC (Bayesian) cater to both paradigms [9].
• Specialized Software: Platforms like JMP and Minitab offer workflows for both classical reliability and (increasingly) Bayesian analysis.

The choice between classical frequency-based and Bayesian belief-based probability is not about identifying a universally superior method, but about selecting the right tool for the specific research context [9].

• Opt for a Classical Approach when: Your analysis requires strict objectivity and standardization, you have large sample sizes, prior information is unavailable or unreliable, and your goal is straightforward hypothesis testing or compliance with regulatory standards that favor p-values and confidence intervals [9].
• Opt for a Bayesian Approach when: You have meaningful prior information (e.g., from experts, previous studies, or simulations), you are dealing with complex models or limited data (common in reliability testing of high-cost systems), you need to make sequential decisions or use adaptive designs, and when the direct probability statements of credible intervals are more intuitive for decision-makers [6] [9].

In practice, the lines are blurring. Many modern analysts advocate for a pragmatic, problem-first perspective, leveraging the strengths of both paradigms. For sensor reliability research, where data is often censored and system complexity is high, the Bayesian paradigm offers a compelling framework for incorporating all available information to make robust inferences about system lifetime and to optimize maintenance strategies.

In the field of sensor reliability analysis and scientific research, two primary statistical paradigms exist for dealing with uncertainty and drawing inferences from data: the classical (frequentist) approach and the Bayesian approach. The fundamental difference between these methodologies hinges on how they treat probability and uncertainty. Classical statistics assumes that probabilities are the long-run frequency of specific events occurring in a repeated series of trials and treats model parameters as fixed, unknown quantities [11] [1]. In contrast, Bayesian statistics provides a framework for updating prior beliefs or knowledge with new evidence, treating probabilities as a measure of belief in a statement's truth and model parameters as random variables [6] [1].

Bayesian methods have gained significant traction in modern research, including sensor reliability, aerospace systems, and drug development, due to their ability to formally incorporate prior knowledge, handle complex models, and provide intuitive probabilistic results [12] [13] [14]. This guide explores the three core components of Bayesian analysis—priors, likelihoods, and posteriors—and provides a structured comparison with classical methods, supported by experimental data and methodologies relevant to research professionals.

The Core Components of Bayesian Analysis

The Bayesian framework is built upon a recursive process of belief updating, formalized by Bayes' theorem. This process integrates three core components to produce a posterior distribution, which encapsulates all knowledge about an unknown parameter after observing data.

Prior Distribution (π(θ)): Quantifying Pre-Existing Knowledge

The prior distribution represents the initial belief about the plausibility of different values of an unknown parameter (θ) before considering the new evidence from the current data [1] [15]. Priors are the cornerstone of the Bayesian approach, allowing for the formal integration of expert opinion, historical data, or results from simulations into the analysis [6] [12].

• Informative Priors: These are used when substantial prior knowledge exists. For example, in reliability engineering, a prior for a failure rate might be constructed from handbook estimates or previous experiments on similar components [15].
• Non-Informative (or Vague) Priors: These are used when prior knowledge is limited, aiming to exert minimal influence on the posterior results. A common example is the uniform distribution, which assigns equal probability to all possible parameter values [6] [15].
• Conjugate Priors: A special class of priors chosen for mathematical convenience, as they yield a posterior distribution that belongs to the same family as the prior. A classic example is using a Beta prior for a binomial likelihood, which results in a Beta posterior [6] [14].

Table 1: Common Conjugate Prior Distributions

Likelihood Model	Parameter	Conjugate Prior	Posterior Hyperparameters
Binomial	Probability of success (θ)	Beta(α, β)	Alpha (α) + successes, Beta (β) + failures [6]
Exponential	Failure rate (λ)	Gamma(α, β)	Alpha (α) + number of failures, Beta (β) + total time [15]
Normal (Known Variance)	Mean (μ)	Normal(μ₀, σ₀²)	A weighted average of prior mean and sample mean [16]

In practice, for a reliability parameter like the probability of a sensor surviving a test (θ), an engineer might choose a Beta prior. Selecting parameters α = 2 and β = 10 expresses a prior belief that θ is likely low, while α = 20 and β = 30 would express a similar prior mean but with much higher confidence [6].

Likelihood (p(x\|θ)): The Weight of the New Evidence

The likelihood function represents the probability of observing the collected data given a specific value of the parameter θ [1]. It quantifies how well different parameter values explain the observed data. In Bayesian analysis, the likelihood is the engine that updates the prior, shifting belief towards parameter values that make the observed data more probable.

The choice of likelihood function is determined by the nature of the data and the underlying process being modeled. Common likelihoods in reliability and sensor research include:

• Bernoulli/Binomial Likelihood: For success/failure or pass/fail data [6].
• Exponential Likelihood: For modeling time-to-failure data with a constant failure rate [15].
• Weibull Likelihood: A more flexible model for time-to-failure data that can account for increasing, decreasing, or constant failure rates [11].
• Normal Likelihood: For continuous measurement data, such as sensor output readings [14].

Posterior Distribution (π(θ\|x)): The Updated Belief

The posterior distribution is the final output of Bayesian analysis. It combines the prior distribution and the likelihood via Bayes' theorem to produce a complete probability distribution for the parameter θ after seeing the data [6] [1]. It is the solution to the problem and contains all information needed for inference.

Bayes' theorem is mathematically expressed as: [ \pi(\theta \mid \mathbf{x}) = \frac{p(\mathbf{x} \mid \theta) \pi(\theta)}{\int p(\mathbf{x} \mid \theta) \pi(\theta) d\theta} \propto p(\mathbf{x} \mid \theta) \pi(\theta) ] In words, the posterior is proportional to the likelihood times the prior [6] [14] [15]. The denominator is a normalizing constant ensuring the posterior distribution integrates to one.

The posterior distribution is the basis for all statistical conclusions, allowing for direct probability statements about parameters. For instance, one can calculate the probability that a sensor's reliability exceeds 0.99 or that the mean time between failures falls within a specific interval [6].

Figure 1: The core workflow of Bayesian inference, showing how the prior and likelihood are combined via Bayes' Theorem to form the posterior distribution.

Experimental Protocols: Implementing Bayesian Analysis in Practice

Applying Bayesian methods to real-world research problems, such as sensor reliability analysis, involves a structured process. The following protocols, drawn from recent research, detail the key methodologies.

Protocol 1: Bayesian Reliability Estimation for Systems with Sparse Data

This protocol is designed for situations with limited physical test data, common in high-cost or high-reliability systems like aerospace sensors [6] [12].

• Formulate the Prior: Elicit an informative prior distribution for the system's reliability (θ). This can be based on expert opinion, subsystem-level test data, or high-fidelity simulations. A Beta distribution is often used for its conjugacy with binomial data. The parameters (α, β) are set to reflect the prior mean (α/(α+β)) and confidence (higher α+β implies higher confidence) [6].
• Define the Likelihood: Conduct a limited number of system-level tests (n), recording the number of successes (x). The likelihood is a Binomial distribution: p(x \| θ) = C(n, x) * θˣ * (1-θ)ⁿ⁻ˣ [6].
• Compute the Posterior: With a Beta(α, β) prior and binomial likelihood, the posterior is a Beta(α + x, β + n - x) distribution. This provides a full probabilistic description of system reliability after testing [6].
• Draw Inference: Calculate posterior summaries such as the mean, median, and 95% credible interval. The probability of exceeding a reliability threshold (e.g., P(θ > 0.95)) can be directly computed from the posterior [6].

Protocol 2: Hierarchical and Multi-Fidelity Data Fusion for Aerospace Systems

This advanced protocol, such as the Integrated Hierarchical Fusion for Mission Reliability Prediction (IHF-MRP), addresses the challenge of integrating heterogeneous data sources (e.g., sparse physical tests and abundant simulation data) for complex, coupled systems [12].

• Model Subsystem Interactions: Instead of relying on predefined reliability block diagrams, establish a data-driven probabilistic mapping from subsystem performance signatures (e.g., sensor anomalies, actuator latency) to overall mission outcomes using a Dirichlet-multinomial model [12].
• Fuse Multi-Fidelity Data: Develop an adaptive weighting mechanism to combine data from different sources (e.g., all-digital simulations, hardware-in-the-loop, flight tests). This mechanism uses a robust sparse-sample Kullback–Leibler (KL) divergence estimator to quantify and account for data fidelity gaps [12].
• Bayesian Updating and Learning: Continuously update the hierarchical model as new test data becomes available. The framework not only predicts mission reliability but also identifies the primary performance drivers and failure modes from the heterogeneous data [12].

Protocol 3: Bayesian Linear Profiling for Chemical Gas Sensor Monitoring

This protocol demonstrates the application of Bayesian methods for quality control and process monitoring in sensor manufacturing [14].

• Data Collection via Neoteric Ranked Set Sampling (NRSS): Collect sensor calibration data using an efficient NRSS scheme instead of simple random sampling to improve the representativeness of the data [14].
• Define Profile Model and Priors: Model the relationship between sensor input and output as a linear profile (a simple linear regression). Specify prior distributions for the profile parameters: intercept, slope, and error variance [14].
• Construct Bayesian Control Charts: Calculate the posterior distributions of the profile parameters. Use these posteriors to construct Bayesian Shewhart, CUSUM, or EWMA control charts. These charts monitor the stability of the sensor's calibration profile over time [14].
• Monitor and Detect Shifts: The process is considered out-of-control if the posterior probability of a parameter shift exceeds a predefined threshold. Bayesian charts have been shown to detect process disturbances more efficiently than their classical counterparts [14].

Comparative Analysis: Bayesian vs. Classical Methods

The following tables provide a structured comparison of classical and Bayesian statistical methods, summarizing their key differences, performance, and applications.

Table 2: Conceptual and Methodological Comparison

Aspect	Classical (Frequentist) Approach	Bayesian Approach
Definition of Probability	Long-run frequency of an event [6] [1]	Degree of belief that a statement is true [6] [1]
Treatment of Parameters	Fixed, unknown constants [11]	Random variables with probability distributions [11]
Use of Prior Information	Not directly incorporated	Formally incorporated via the prior distribution [15]
Primary Output	Point estimate and confidence interval [11]	Full posterior distribution [16]
Interpretation of Uncertainty	A 95% CI means: with repeated sampling, 95% of such intervals will contain the true parameter. It does not quantify the probability of the parameter [1].	A 95% Credible Interval means: there is a 95% probability that the true parameter lies within this interval, given the data and prior [16].

Table 3: Performance Comparison in Reliability & Sensor Applications

Metric	Classical Methods	Bayesian Methods	Supporting Evidence
Small-Sample Performance	Struggles with sparse data; MLE can be unstable or undefined (e.g., with zero failures) [6] [11].	Excels by leveraging prior information; provides meaningful estimates even with no observed failures [6] [11].	Simulation studies show Bayesian methods provide more stable estimates with n < 30 [11].
Uncertainty Quantification	Relies on asymptotic approximations (e.g., normal approximation for MLE) which can be poor with small samples [15].	Provides exact, finite-sample uncertainty from the posterior distribution; more consistent [15].	In failure-censored sampling, Bayesian credible intervals provided more robust coverage than classical intervals under small samples [4].
Computational Complexity	Generally computationally efficient (e.g., MLE) [11].	Can be computationally intense, requiring MCMC or variational inference for complex models [11] [16].	Noted as a key challenge, especially for large datasets and complex hierarchical models [16].
Handling Complex Systems	Limited by assumptions of subsystem independence and binary states [12].	Superior for modeling coupled interactions and continuous performance signatures via hierarchical models [12].	IHF-MRP framework successfully predicted missile intercept reliability by fusing multi-fidelity data [12].
Process Monitoring	Assumes process parameters are fixed, which is less practical under parameter uncertainty [14].	Efficiently handles parameter uncertainty; Bayesian control charts show faster detection of process shifts [14].	Bayesian EWMA charts for linear profiles detected smaller shifts more quickly than classical charts in a sensor monitoring case study [14].

The Scientist's Toolkit: Essential Reagents for Bayesian Reliability Experiments

For researchers implementing the protocols described, the following "reagents" are essential computational and methodological components.

Table 4: Key Research Reagents for Bayesian Analysis

Reagent Solution	Function in the Analysis
Beta Distribution	A versatile conjugate prior and posterior model for probabilities and reliabilities bounded between 0 and 1 [6] [4].
Markov Chain Monte Carlo (MCMC)	A class of algorithms (e.g., Metropolis-Hastings, Gibbs Sampling) used to generate samples from complex posterior distributions when analytical solutions are intractable [11] [15].
Gaussian Process (GP) Prior	A flexible prior used to model unknown functions or spatial/temporal correlations, such as inferring a plasma current density distribution from magnetic sensor data [17].
Dirichlet-Multinomial Model	A hierarchical model used to establish probabilistic mappings from multiple discrete inputs (e.g., subsystem performance states) to categorical outcomes (e.g., mission success/failure) [12].
Kullback-Leibler (KL) Divergence Estimator	An information-theoretic measure used in multi-fidelity data fusion to quantify the discrepancy between data sources and compute adaptive weights [12].
Ptaquiloside	Ptaquiloside, CAS:87625-62-5, MF:C20H30O8, MW:398.4 g/mol
Bakkenolide III	Bakkenolide III

Figure 2: A data fusion workflow for complex system reliability prediction, integrating diverse data sources within a hierarchical Bayesian model.

The choice between classical and Bayesian methods is not merely a technicality but a fundamental decision that shapes the approach to uncertainty in research. Classical statistics offers computational efficiency and objectivity in data-rich environments. However, the Bayesian paradigm, with its core components of priors, likelihoods, and posteriors, provides a powerful, coherent framework for updating beliefs with evidence.

As demonstrated in sensor reliability, aerospace, and pharmaceutical applications, the strengths of Bayesian methods are particularly evident when dealing with complex systems, limited data, and the need to formally incorporate diverse sources of information. The ability to provide direct probabilistic interpretations and to seamlessly integrate multi-fidelity data makes Bayesian analysis an indispensable tool for modern researchers and scientists striving to make robust inferences under uncertainty.

Analytical Frameworks for Sensor Reliability

In biomedical applications, from implantable devices to wearable sensors, ensuring long-term reliability is paramount for accurate diagnosis and effective patient monitoring. The analysis of sensor reliability often hinges on interpreting time-to-failure data, which is frequently censored; meaning the complete failure time for all units is not always observable within a study period. Statistical methods are essential to draw valid inferences from such incomplete data. Two predominant philosophical frameworks exist for this analysis: the Classical (or Frequentist) approach and the Bayesian approach.

The core distinction lies in how each framework handles uncertainty and prior knowledge. Classical statistics treats parameters as fixed unknown constants to be estimated solely from the observed data. In contrast, Bayesian statistics formally incorporates prior knowledge or beliefs about parameters, which are updated with observed data to form a posterior distribution [1]. This fundamental difference shapes their application in biomedical sensor reliability, influencing how study designs are structured, risks are quantified, and conclusions are drawn for critical decision-making in drug development and clinical research.

Comparative Analysis: Classical versus Bayesian Methods

The following table summarizes the core characteristics of the Classical and Bayesian approaches as applied to reliability assessment.

Table 1: Fundamental Comparison of Classical and Bayesian Methods for Reliability Analysis

Feature	Classical (Frequentist) Approach	Bayesian Approach
Philosophical Basis	Probabilities represent long-run frequencies of events in repeated trials [1].	Probabilities represent a degree of belief or certainty about an event, which is updated as new data arrives [1].
Parameter Treatment	Parameters (e.g., mean failure rate) are fixed, unknown constants.	Parameters are random variables described by probability distributions.
Use of Prior Information	Does not formally incorporate prior knowledge or beliefs.	Explicitly incorporates prior knowledge via a "prior distribution," which is updated with data to form the "posterior distribution" [1].
Output & Interpretation	Provides point estimates and confidence intervals. A 95% confidence interval means that if the experiment were repeated many times, 95% of such intervals would contain the true parameter.	Provides a full posterior probability distribution for parameters. A 95% credible interval means there is a 95% probability the true parameter lies within that interval, given the data and prior.
Computational Complexity	Generally less computationally intensive (e.g., Maximum Likelihood Estimation).	Often more computationally intensive, relying on Markov Chain Monte Carlo (MCMC) methods for complex models [1].

The practical performance of these methods has been quantitatively compared in various studies. Research on the Weighted Lindley distribution under unified hybrid censoring schemes, relevant for survival and reliability data, demonstrated that Bayesian estimators consistently yielded lower Mean Squared Errors (MSEs) than classical Maximum Likelihood Estimators (MLEs). Furthermore, the Bayesian credible intervals were generally narrower than the frequentist confidence intervals [18]. Similarly, in the context of optimizing failure-censored sampling plans for lognormal lifetime models, Bayesian methods were found to provide more robust designs, especially when prior information is uncertain [4].

Table 2: Quantitative Performance Comparison from Reliability Studies

Study Context	Performance Metric	Classical Method	Bayesian Method
Weighted Lindley Distribution under Censoring [18]	Estimator Accuracy (Mean Squared Error)	Higher	Lower
Weighted Lindley Distribution under Censoring [18]	Interval Estimate Width	Wider	Narrower
Locomotive Wheel-Set Reliability Analysis [5]	Utility for Preventive Maintenance	Effective, uses ALT & DOE	Effective, uses semi-parametric models with Gamma frailties
Lognormal Sampling Plans [4]	Robustness under Parameter Uncertainty	Greater sensitivity to changes	More robust designs

Experimental Protocols for Method Comparison

To objectively compare classical and Bayesian methods in a biomedical sensor context, a structured experimental and analytical protocol is essential. The following workflow outlines the key stages, from data collection to inference, highlighting where the methodological approaches diverge.

Core Experimental Components

The reliability analysis of biomedical sensors relies on several key components and methodologies, as evidenced by real-world studies and reviews.

Table 3: Research Reagent Solutions for Sensor Reliability Analysis

Component / Solution	Function in Reliability Analysis	Example from Literature
Unified Hybrid Censoring Scheme (UHCS)	A versatile framework integrating multiple censoring strategies to efficiently collect and analyze lifetime data under resource constraints [18].	Used to evaluate the Weighted Lindley distribution for modeling sensor lifetime data, allowing experiments to be terminated based on either a pre-set time or a pre-set number of failures [18].
Markov Chain Monte Carlo (MCMC)	A computational algorithm used in Bayesian analysis to sample from the complex posterior probability distribution of parameters, enabling inference [5].	Employed in a Bayesian semi-parametric degradation approach for locomotive wheel-sets to establish lifetime using degradation data and explore the influence of unobserved covariates [5].
Piecewise Constant Hazard Model with Gamma Frailties	A semi-parametric Bayesian survival model that does not assume a specific shape for the hazard function over time. Frailties account for unobserved heterogeneity or dependencies between units (e.g., sensors on the same device) [5].	Applied to model the dependency of wheel-set degradation based on their installed position (bogie) on a locomotive, revealing that the specific bogie had more influence on lifetime than the axle or side [5].
Bayesian Structural Time Series (BSTS)	A framework for modeling time series data to evaluate the causal impact of an intervention by constructing a counterfactual (what would have happened without the intervention) [19].	Proposed for analyzing mobile health and wearable sensor data to quantify the impact of a health intervention (e.g., exercise on blood glucose) by correcting for complex covariate structures and temporal patterns [19].

Detailed Protocol: A Case Study in Method Comparison

The following protocol is adapted from a comparative study on the Weighted Lindley distribution, which is directly applicable to modeling sensor lifetime data [18].

• Study Design and Data Collection:

  • A sample of n identical biomedical sensors is placed on a life-testing platform.
  • A Unified Hybrid Censoring Scheme (UHCS) is implemented. This means the test will terminate at a random time T* = min{max(X_{m}, T1), T2}, where T1 and T2 are pre-set times (T1 < T2), and X_{m} is the time of the m-th failure. This scheme efficiently combines Type-I and Type-II censoring.

• Classical (Frequentist) Analysis:

  • Parameter Estimation: The Maximum Likelihood Estimation (MLE) method is used. The likelihood function is constructed based on the observed censored data, and numerical optimization techniques (e.g., Newton-Raphson) are applied to find the parameter values that maximize this function.
  • Interval Estimation: Asymptotic Confidence Intervals for the parameters are derived based on the observed Fisher information matrix. This relies on the large-sample property that MLEs are normally distributed.

• Bayesian Analysis:

  • Prior Selection: Informative or non-informative prior distributions (e.g., Gamma, Uniform) are specified for the model parameters, reflecting prior knowledge or belief about their values before the experiment.
  • Posterior Computation: The posterior distribution is computed by combining the prior distributions with the likelihood of the observed data using Bayes' Theorem. Since an analytical solution is often intractable, Markov Chain Monte Carlo (MCMC) methods like the Gibbs sampler or Metropolis-Hastings algorithm are used to generate samples from the posterior distribution.
  • Inference: Point estimates (e.g., posterior mean or median) and Bayesian Credible Intervals (e.g., Highest Posterior Density intervals) are computed directly from the MCMC samples.

• Performance Comparison:

  • A Monte Carlo simulation is run, repeating the above process hundreds or thousands of times to compare the methods.
  • Key performance metrics are calculated and compared, including:
    • Mean Squared Error (MSE): Average squared difference between the estimated and true parameter values. Lower MSE indicates better accuracy.
    • Interval Width: The average width of the confidence/credible intervals. Narrower intervals indicate greater precision.
    • Coverage Probability: The proportion of times the confidence/credible interval contains the true parameter value.

This structured protocol allows for a direct, quantitative comparison of the robustness and efficiency of classical versus Bayesian methods in a controlled, yet realistic, biomedical sensor testing environment.

The comparison between classical and Bayesian methods for biomedical sensor reliability is not about declaring a universal winner. Each offers distinct advantages. The Bayesian approach, with its ability to formally incorporate prior information and provide intuitive probabilistic outputs, often leads to more precise estimates and robust designs, particularly with limited data or well-understood failure mechanisms [18] [4]. The Classical approach remains a powerful, straightforward tool, especially when prior knowledge is absent or when its objectivity is required for regulatory purposes.

Future research will be shaped by several key trends. The rise of digital twins—virtual patient models dynamically updated with real-time sensor data—for precision medicine will place new demands on VVUQ (Verification, Validation, and Uncertainty Quantification) processes. Here, Bayesian frameworks are uniquely positioned to continuously update model predictions and quantify uncertainty in a clinically actionable way [20]. Furthermore, the integration of ensemble learning and AI with traditional reliability models promises to enhance the classification and prediction of complex failure patterns from multi-modal sensor data [21] [19]. For researchers and drug development professionals, the choice of method will ultimately depend on the specific application, the quality of prior knowledge, and the required form of inference for decision-making.

The Role of Uncertainty in Sensor Data and Model Predictions

In modern technological systems, from autonomous vehicles to industrial manufacturing, the reliability of sensor data is paramount for ensuring proper functioning and safety [22]. However, sensor data is inherently afflicted by various sources of uncertainty that can compromise the accuracy and reliability of model predictions. These uncertainties become particularly critical in applications like medical device monitoring, pharmaceutical manufacturing, and drug development, where decision-making depends on highly accurate sensor readings. The random deviations present in sensor measurements contribute significantly to overall measurement uncertainty, presenting substantial challenges for data interpretation and model performance [23].

The field of reliability engineering has developed two principal statistical paradigms to address these challenges: classical (frequentist) and Bayesian inference methods [11]. Classical approaches treat model parameters as fixed but unknown quantities and use techniques like maximum likelihood estimation to draw inferences from observed data. In contrast, Bayesian methods treat parameters as random variables with associated probability distributions, allowing for the incorporation of prior knowledge which is updated through Bayes' theorem as new data becomes available [11]. Understanding the strengths, limitations, and appropriate applications of each framework is essential for researchers and professionals working with sensor-derived data in scientific and industrial contexts.

Theoretical Foundations of Uncertainty

Typology of Uncertainty

In supervised machine learning and predictive modeling, uncertainty is broadly categorized into two primary types: aleatoric and epistemic uncertainty [24]. Aleatoric uncertainty refers to the inherent randomness or noise in the data generation process itself. This type of uncertainty is irreducible, meaning it cannot be diminished by collecting more data or improving models. In sensor systems, aleatoric uncertainty manifests as sensor noise, measurement errors, motion blur in cameras, or signal quantization errors [25]. For example, a camera may produce blurred images due to rapid movement, while radar systems exhibit signal noise from electrical interference.

Epistemic uncertainty, conversely, stems from incomplete knowledge or information about the system being modeled [24]. This includes limitations in the model structure, insufficient training data, or lack of coverage of all possible operational states. Unlike aleatoric uncertainty, epistemic uncertainty can be reduced by gathering more data, improving model architectures, or incorporating additional domain knowledge [25]. A practical example includes a self-driving car encountering unfamiliar weather conditions or a drone discovering previously unobserved objects in its environment.

Multiple factors contribute to uncertainty in sensor-based systems, each requiring specific mitigation strategies:

• Sensor Noise and Bias: Every sensor introduces measurement noise, which is unpredictable and random in nature [25]. This includes phenomena like motion blur in cameras, signal noise in radar systems, and quantization errors in image sensors. Bias represents a systematic shift in measurements that affects all readings consistently in one direction.

• Temporal and Spatial Misalignment: In multi-sensor systems, different sensors may capture measurements at varying times and from different physical locations [25]. A camera might capture an image at one moment, while a radar scan occurs milliseconds later. Without proper synchronization and alignment, this can lead to positional discrepancies that introduce uncertainty in object localization.

• Data Association Errors: When multiple objects move within a sensor's field of view, correctly associating sensor readings with specific objects becomes challenging [25]. This problem is exacerbated when sensors have different resolutions or when objects occupy overlapping areas in the sensor data.

• Environmental Factors: Extreme conditions during manufacturing or operation, such as vibration, temperature fluctuations, and humidity variations, can degrade sensor performance and introduce uncertainty into the data [23].

Classical Methods for Uncertainty Quantification

Fundamental Principles

Classical (frequentist) approaches to uncertainty quantification treat model parameters as fixed but unknown quantities that must be estimated from observed data [11]. These methods rely heavily on statistical techniques such as maximum likelihood estimation (MLE), confidence intervals, and hypothesis testing to draw inferences about the underlying system. The classical framework assumes that parameters have true values that remain constant, and any uncertainty arises solely from sampling variability rather than inherent randomness in the parameters themselves.

In reliability engineering, classical methods have served as the cornerstone for decades, with techniques like Non-Homogeneous Poisson Processes (NHPP) modeling time-varying failure rates and the Kaplan-Meier estimator handling censored data in reliability testing [11]. These approaches are computationally efficient, widely implemented in industrial standards, and provide straightforward interpretation through point estimates and confidence intervals.

Implementation Approaches

Confidence Intervals for Uncertainty Quantification: A prominent classical approach for sensor data-driven prognosis utilizes confidence intervals based on z-scores to quantify prediction uncertainty [26]. The confidence interval is calculated as:

$$ CI = \bar{X} \pm z \cdot \frac{\omega}{\sqrt{n}} $$

where $\bar{X}$ represents the sample mean, $z$ is the z-score associated with a chosen confidence level (e.g., 2.5758 for 99% confidence), $\omega$ signifies the standard deviation, and $n$ is the number of data points [26]. The interval width ($CI_w = 2z \cdot \frac{\omega}{\sqrt{n}}$) serves as a direct metric for uncertainty, with narrower intervals indicating higher confidence in predictions [26].

Experimental Protocol for Vibration Signal Analysis: In a practical implementation for bearing degradation monitoring, researchers generated synthetic vibration signals mimicking real-world sensor data [26]. The mathematical model incorporated an exponentially growing sinusoidal pattern with additive Gaussian noise and outliers:

$$ X = A \sin(2\pi f T) \cdot e^{-\lambda \bar{T}} + \mu + \rho $$

where $A$ represents amplitude, $f$ is oscillation frequency, $\lambda$ denotes the decay rate, $\mu$ is Gaussian noise, and $\rho$ represents outliers [26]. The health index $Y$ was modeled as a linearly decreasing function: $Y_i = 1 - \frac{i}{n}$ for $i = 1, 2, ..., n$.

The experimental workflow involved:

• Time vector formulation with a predetermined number of points
• Generation of composite sensor signals with exponential decay oscillations
• Introduction of Gaussian noise and outliers to simulate real measurement conditions
• Health index calculation representing progressive system degradation
• Data splitting using an 80-20 train-test validation approach
• Model training with optimization targeting confidence interval width minimization [26]

Bayesian Methods for Uncertainty Quantification

Fundamental Principles

Bayesian methods adopt a fundamentally different perspective by treating unknown parameters as random variables with associated probability distributions rather than fixed quantities [11]. This framework incorporates prior knowledge—such as expert opinion, historical data, or domain expertise—which is then updated with observational data through Bayes' theorem to form posterior distributions. The Bayesian approach is particularly valuable in scenarios involving limited data, expert judgment, or the need for probabilistic decision-making under uncertainty [11].

The mathematical foundation of Bayesian inference rests on Bayes' theorem:

$$ P(\theta|D) = \frac{P(D|\theta) \cdot P(\theta)}{P(D)} $$

where $P(\theta|D)$ represents the posterior distribution of parameters $\theta$ given data $D$, $P(D|\theta)$ is the likelihood function, $P(\theta)$ is the prior distribution encapsulating previous knowledge, and $P(D)$ serves as the normalizing constant.

Implementation Approaches

Bayesian Model Fusion: This technique leverages Bayesian probability theory to fuse predictions from multiple models, creating a probabilistic ensemble that enhances predictive accuracy while quantifying uncertainty [27]. The implementation involves calculating likelihoods from individual model predictions, applying prior weights to each model, and computing posterior probabilities through weighted aggregation [27].

A practical implementation for image classification using MNIST data demonstrated this approach with three different models: Support Vector Classifier (SVC), K-Nearest Neighbors (KNN), and Logistic Regression (LR) [27]. The Bayesian fusion process computed posteriors as:

$$ \text{posteriors} = \sum(\text{noisy_likelihoods} \cdot \text{priors}[:, \text{np.newaxis}, \text{np.newaxis}]) $$

The uncertainty was then quantified using entropy calculated from the posterior probabilities: $-\sum(\text{probs} \cdot \log_2(\text{probs} + 10^{-15}))$ [27].

Bayesian Reliability Estimation: For reliability testing with Type II censoring, Bayesian methods provide robust frameworks for estimating system reliability parameters [4]. In this context, the defect rate $p$ is treated as a random variable following a Beta distribution, which serves as a conjugate prior to the binomial distribution, simplifying posterior computation [4]. The approach is particularly valuable when traditional acceptance sampling assumes fixed defect rates, while in reality, defect rates may vary across batches due to material differences, processing conditions, or environmental factors.

Comparative Analysis: Classical vs. Bayesian Methods

Performance Comparison

Table 1: Comparative Analysis of Classical and Bayesian Methods for Sensor Reliability Analysis

Aspect	Classical Methods	Bayesian Methods
Parameter Treatment	Parameters as fixed, unknown quantities [11]	Parameters as random variables with probability distributions [11]
Prior Knowledge	Does not incorporate prior knowledge	Explicitly incorporates prior knowledge through prior distributions [11]
Uncertainty Representation	Confidence intervals based on hypothetical repeated sampling [26]	Posterior distributions and credible intervals with probabilistic interpretation [27]
Computational Complexity	Generally computationally efficient [11]	Can become computationally intensive, especially with many models and data points [27]
Data Requirements	Relies on large sample sizes for stable inferences [11]	Effective with small sample sizes, leveraging prior information [11]
Handling of Censored Data	Uses specialized estimators (e.g., Kaplan-Meier) [11]	Naturally incorporates censoring through likelihood construction [4]
Interpretation	Straightforward interpretation of point estimates and confidence intervals [11]	Probabilistic interpretation directly addressing parameter uncertainty [27]

Table 2: Experimental Results from Vibration-Based Prognosis Study [26]

Metric	LSTM (RMSE Objective)	LSTM (Uncertainty Quantification Objective)
Confidence Interval Width	Wider and less stable intervals	Tighter and more stable confidence intervals
Prediction Residuals	Larger deviations from true values	Closer to zero on average
Uncertainty Estimation	Less reliable uncertainty estimates	Improved uncertainty estimation and model calibration
Robustness	More sensitive to data variations	Enhanced robustness against data variations

Case Study: Reliability Testing with Type II Censoring

A comparative study on failure-censored sampling plans for lognormal lifetime models examined both classical and Bayesian risks in optimal experimental design [4]. The research focused on how variations in prior distributions, specifically beta distributions for defect rates, influence producer's risk, consumer's risk, and optimal sample size.

The experimental protocol involved:

• System Modeling: Lifetime $T$ of electronic components followed a two-parameter lognormal distribution, with logarithmic lifetime $X = \log(T)$ following a normal distribution with parameters $(\mu, \sigma)$ [4]
• Censoring Mechanism: Tests were terminated after a predetermined number of failures ($m$), with censoring rate defined as $q = 1 - \frac{m}{n}$ [4]
• Parameter Estimation: For classical methods, maximum likelihood estimation was used, while Bayesian approaches employed Markov Chain Monte Carlo (MCMC) techniques for posterior sampling [4]
• Risk Assessment: Both producer's risk (rejecting conforming products) and consumer's risk (accepting non-conforming products) were evaluated under both frameworks [4]

The results demonstrated that Bayesian methods generally provided more robust experimental designs under uncertain prior information, while classical methods exhibited greater sensitivity to parameter changes [4]. Bayesian approaches allowed for more effective balancing of sample size constraints with risk control objectives, particularly in small-sample scenarios common in reliability testing of high-reliability components.

Methodological Workflows

Classical Method Workflow for Sensor Reliability

Classical Reliability Analysis Workflow

Bayesian Method Workflow for Sensor Reliability

Bayesian Reliability Analysis Workflow

Research Reagent Solutions and Materials

Table 3: Essential Research Tools for Sensor Reliability Experiments

Tool/Category	Specific Examples	Function in Research
Statistical Software	R, Python (Scikit-learn, PyMC3, TensorFlow Probability)	Implementation of classical and Bayesian statistical models for reliability analysis [27] [26]
Sensor Simulation Tools	Large Eddy Simulation (LES), Computational Aeroacoustics (CAA)	Generating synthetic sensor data for method validation under controlled conditions [28]
Reliability Testing Platforms	Accelerated Life Testing Systems, Environmental Chambers	Subjecting sensors to controlled stress conditions to collect failure time data [11]
Uncertainty Quantification Libraries	TensorFlow Uncertainty, Uber Pyro, Stan	Implementing Bayesian neural networks, Monte Carlo dropout, and probabilistic deep learning models [27] [26]
Data Annotation Platforms	Human-in-the-Loop annotation systems	Providing high-quality labeled data for training uncertainty-aware models [25]
Optimization Frameworks	Bayesian Optimization, Hyperopt	Tuning hyperparameters of machine learning models with uncertainty considerations [26]

The comparative analysis of classical and Bayesian methods for sensor reliability analysis reveals distinct advantages and limitations for each approach. Classical methods offer computational efficiency, straightforward interpretation, and well-established implementation protocols, making them suitable for applications with abundant data and minimal prior knowledge [11]. Their reliance on large-sample properties and fixed-parameter assumptions, however, can limit their effectiveness in small-sample scenarios or when incorporating expert judgment is essential.

Bayesian methods excel in contexts characterized by limited data, the need to incorporate prior knowledge, and requirements for probabilistic interpretation of parameters [11] [4]. The ability to provide full posterior distributions rather than point estimates offers more comprehensive uncertainty quantification, particularly valuable in critical applications where understanding confidence in predictions is as important as the predictions themselves [27]. The computational demands of Bayesian methods and the challenge of specifying appropriate prior distributions remain practical considerations for implementation.

For researchers and professionals in drug development and pharmaceutical applications, the choice between classical and Bayesian approaches should be guided by specific application requirements, data availability, and decision-making context. Bayesian methods are particularly well-suited for applications incorporating historical data or expert knowledge, while classical approaches offer efficiency and simplicity when dealing with large, representative datasets. Hybrid approaches that leverage the strengths of both paradigms present promising avenues for future research in sensor reliability analysis.

Practical Implementation: From Bernoulli Trials to Complex System Modeling

In reliability engineering, sensor development, and pharmaceutical research, statistical analysis of success/no-success data—often termed "Bernoulli trials"—is fundamental for determining product reliability, treatment efficacy, and system performance. The classical binomial model and Bayesian beta-binomial model represent two philosophically and methodologically distinct approaches to this analysis. The binomial model operates within the frequentist paradigm, treating parameters as fixed unknown quantities to be estimated solely from collected data [29]. In contrast, the beta-binomial model operates within the Bayesian framework, explicitly incorporating prior knowledge or expert belief into the analysis while providing a natural mechanism to account for overdispersion—the common phenomenon where observed data exhibits greater variability than predicted by simple binomial sampling [30] [31].

The choice between these methodologies carries significant implications for research conclusions, particularly in fields with high-stakes decision-making such as medical device validation and drug development. This guide provides an objective comparison of these competing approaches, examining their theoretical foundations, implementation requirements, and performance characteristics to inform methodological selection in reliability and development research contexts.

Theoretical Foundations and Mathematical Frameworks

The Classical Binomial Model

The classical binomial model represents the frequentist approach to analyzing binary outcome data. It assumes that each trial is independent and identically distributed, with a constant, fixed probability of success across all trials.

Mathematical Formulation: For ( n ) independent trials with a fixed probability of success ( \theta ), the probability of observing ( y ) successes is given by: [ P(Y = y | \theta) = \binom{n}{y} \theta^y (1-\theta)^{n-y} ] where ( \theta ) is treated as an unknown but fixed parameter [29]. Estimation typically proceeds via maximum likelihood estimation (MLE), yielding the intuitive estimator ( \hat{\theta}_{MLE} = y/n ). Confidence intervals are constructed to express the frequency properties of the estimation procedure, interpreted as the long-run coverage probability across repeated sampling.

The Bayesian Beta-Binomial Model

The Bayesian beta-binomial model reformulates the problem by treating the parameter ( \theta ) as a random variable with its own probability distribution, enabling researchers to incorporate prior knowledge formally into the analysis.

Mathematical Formulation: The model uses a beta distribution as the conjugate prior for the binomial likelihood: [ \begin{align} \text{Prior:} \quad & \theta \sim \text{Beta}(\alpha, \beta) \ \text{Likelihood:} \quad & Y | \theta \sim \text{Bin}(n, \theta) \ \text{Posterior:} \quad & \theta | y \sim \text{Beta}(\alpha + y, \beta + n - y) \end{align} ] where ( \alpha ) and ( \beta ) are hyperparameters that characterize prior beliefs about the success probability [32] [29]. The posterior distribution combines prior knowledge with empirical evidence, with the relative influence of each determined by the sample size and the concentration of the prior.

The beta-binomial model naturally accommodates overdispersion through its hierarchical structure. When population heterogeneity exists—violating the binomial assumption of constant success probability—the beta-binomial provides a better fit by modeling this extra-binomial variation [30] [31].

Methodological Comparison and Experimental Evaluation

Fundamental Philosophical and Practical Differences

Table 1: Core Conceptual Differences Between Binomial and Beta-Binomial Models

Aspect	Classical Binomial Model	Bayesian Beta-Binomial Model
Parameter Interpretation	Fixed unknown constant	Random variable with distribution
Prior Information	Not incorporated	Explicitly incorporated via prior distribution
Output	Point estimate and confidence interval	Full posterior distribution
Uncertainty Quantification	Frequency-based (sampling distribution)	Probability-based (credible intervals)
Overdispersion Handling	Cannot accommodate	Naturally handles through hierarchical structure
Computational Complexity	Generally simple	Often requires MCMC for complex extensions

Experimental Performance Comparison

Experimental studies have systematically evaluated the performance of both approaches under various conditions, particularly focusing on estimation accuracy and uncertainty quantification.

Table 2: Experimental Performance Comparison Based on Simulation Studies

Performance Metric	Classical Binomial Model	Bayesian Beta-Binomial Model
Bias in Small Samples	High when data are sparse	Reduced with informative priors
Variance Estimation	Often underestimated with overdispersion	More accurate with overdispersion
Coverage Probability	Below nominal level with model violations	Closer to nominal with appropriate priors
Influence of Prior	Not applicable	Significant with small samples, diminishes with large samples
Handling of Zero Events	Problematic (zero estimate)	Accommodated through prior

Research by Palm et al. demonstrated that the beta-binomial model "outperforms the usual ARMA- and Gaussian-based detectors" in signal detection applications, highlighting its superior performance in specific inferential contexts [33]. In reliability engineering, Bayesian approaches have proven particularly valuable for high-reliability systems where failures are rare, as they can formally incorporate information from similar systems, expert opinion, or previous generations of a product [34] [35].

Detailed Experimental Protocol for Method Comparison

To objectively compare these methodologies in practice, researchers can implement the following experimental protocol:

Step 1: Data Generation

• Simulate binary outcome data under varying conditions: (a) ideal binomial conditions (constant θ), (b) with overdispersion (θ varying across subgroups), and (c) with small sample sizes (n < 30)
• For overdispersed scenarios, implement a beta-binomial data generation process where θ ~ Beta(α,β) and then Y | θ ~ Bin(n,θ)

Step 2: Model Implementation

• For classical binomial: Compute MLEs and Wald-type 95% confidence intervals
• For beta-binomial: Implement with both weakly informative (Beta(1,1)) and moderately informative priors (e.g., Beta(3,1) for high-reliability scenarios)
• Use Markov Chain Monte Carlo (MCMC) methods for posterior sampling if closed-form solutions are unavailable

Step 3: Performance Evaluation

• Calculate empirical bias: ( \frac{1}{N}\sum{i=1}^N (\hat{\theta}i - \theta_{true}) )
• Compute mean squared error: ( \frac{1}{N}\sum{i=1}^N (\hat{\theta}i - \theta_{true})^2 )
• Evaluate coverage probability: proportion of simulations where confidence/credible intervals contain θtrue
• Assess interval width: average length of confidence/credible intervals

This protocol mirrors approaches used in rigorous methodological comparisons, such as those described by Harrison who evaluated models "under various degrees of overdispersion" and across "a range of random effect sample sizes" [30].

Implementation Workflows and Computational Tools

Analytical Workflows

The conceptual and analytical workflows for implementing these approaches differ significantly, as illustrated below:

Table 3: Essential Tools for Implementing Binomial and Beta-Binomial Analyses

Tool Category	Specific Solutions	Application Context
Statistical Software	R, Python, Stan, JAGS	General implementation
R Packages	binom, VGAM, emdbook	Classical binomial analysis
Bayesian R Packages	rstanarm, brms, MCMCpack	Beta-binomial modeling
Diagnostic Tools	Posterior predictive checks, residual plots	Model validation
Prior Elicitation	SHELF protocol, prior predictive checks	Informed prior specification

For reliability applications with limited data, Botts emphasizes that Bayesian methods are particularly valuable as they "enable inclusion of other types of data (such as computer simulation experiments or subject-matter-expert opinions)" [6]. This capability is crucial in fields like pharmaceutical development and high-reliability engineering where ethical constraints, cost, or rarity of events limits sample sizes.

Application in Sensor Reliability and Drug Development Contexts

Sensor Reliability Analysis

In sensor reliability assessment, researchers often encounter scenarios with limited failure data, especially for high-reliability components. The Bayesian approach provides a formal mechanism to incorporate information from accelerated life tests, similar component types, or physics-based models. For example, a study on hierarchical Bayesian modeling demonstrated that "choosing strong informative priors leads to distinct predictions, even if a larger sample size is considered" [34]. This property is particularly valuable when assessing conformance to reliability requirements with minimal testing.

In a three-state reliability model (normal, potential failure, functional failure), Bayesian methods allow integration of multi-source prior information, addressing the "contradiction between small test samples and high reliability requirements" that directly impacts development costs and timelines [35].

Pharmaceutical Development Applications

In drug development, success/no-success data arises in various contexts including toxicology studies, clinical trial endpoints, and manufacturing quality control. The beta-binomial model's ability to handle overdispersion makes it particularly valuable for multi-center clinical trials where patient populations or practice patterns may introduce variability beyond simple binomial sampling.

Bayesian approaches also facilitate adaptive trial designs through natural incorporation of accumulating evidence, potentially reducing development costs and time-to-market while maintaining rigorous decision standards. The explicit quantification of uncertainty via posterior distributions supports more nuanced risk-benefit assessments in regulatory submissions.

The choice between classical binomial and Bayesian beta-binomial models involves trade-offs between philosophical frameworks, implementation complexity, and inferential goals. The classical binomial model offers simplicity, computational efficiency, and familiar interpretation, performing well when the binomial assumptions are met and sample sizes are adequate. Conversely, the Bayesian beta-binomial model provides greater flexibility for incorporating prior knowledge, naturally handles overdispersion, and offers more intuitive uncertainty quantification through credible intervals.

For research applications, selection guidelines include:

• Use classical binomial when prior information is unavailable or incorporation is undesirable, data follow binomial assumptions, and rapid implementation is prioritized
• Prefer beta-binomial when prior information exists, sample sizes are small, overdispersion is suspected, or intuitive probability statements about parameters are desired

In sensor reliability and drug development contexts where testing is costly and failures are rare, the Bayesian approach offers distinct advantages through formal information integration. As with any methodological choice, model assumptions should be validated against empirical data, and sensitivity analyses conducted—particularly for prior specification in Bayesian applications.

In sensor reliability analysis, the choice between classical (frequentist) and Bayesian statistical paradigms profoundly influences model robustness, interpretability, and practical utility. While classical methods offer established, data-driven approaches without requiring prior knowledge, Bayesian methods explicitly incorporate expert opinion and historical data through prior distributions, enabling a more nuanced handling of uncertainty. This guide provides a structured comparison of these frameworks, focusing on their application in sensor data fusion and reliability evaluation. Supported by experimental protocols and quantitative data comparisons, we demonstrate that Bayesian approaches, particularly those utilizing hierarchical models and contextual discounting, offer superior adaptability in dynamic environments and enhanced performance in data-scarce scenarios. The synthesis aims to equip researchers and engineers with the knowledge to select and implement the most appropriate methodology for their specific reliability analysis challenges.

Sensor reliability analysis is a cornerstone of robust multi-sensor data fusion systems, which are critical in fields ranging from target recognition and industrial monitoring to complex network management. These systems combine information from multiple sensors to form a more accurate and coherent perception of the environment than any single sensor could provide. However, sensor data is inherently imperfect, contaminated by environmental noise, deceptive target behaviors, and hardware limitations. Effectively managing this uncertainty and the inherent reliability of each sensor is a fundamental challenge. The Dempster-Shafer Evidence Theory (Evidence Theory) and Bayesian probability have emerged as two powerful, yet philosophically distinct, frameworks for representing and reasoning with such imperfect information [36] [37].

The core divergence between classical and Bayesian methods lies in their treatment of uncertainty and unknown parameters. Classical (frequentist) approaches treat sensor reliability parameters as fixed, unknown quantities to be estimated solely from observed data. Inference relies on long-run frequency properties, such as the performance of an estimator over many hypothetical repeated experiments. In contrast, the Bayesian framework treats all unknown parameters as random variables with associated probability distributions. This allows for the formal incorporation of pre-existing knowledge—whether from expert opinion or historical data—through prior distributions, which are then updated with new observational data via Bayes' theorem to yield posterior distributions [38] [39]. This article provides a comprehensive comparison of these two paradigms within the context of sensor reliability analysis, offering experimental protocols, data-driven comparisons, and practical guidance for researchers and engineers.

Theoretical Framework: Classical vs. Bayesian Methods

The Classical (Frequentist) Paradigm

Classical methods in sensor reliability are built on the principle of long-run frequency. A sensor's reliability is a fixed property, and statistical methods aim to estimate it without recourse to prior beliefs.

• Philosophical Basis: Probability is defined as the limit of the relative frequency of an event after a large number of trials. Unknown parameters, such as a sensor's failure rate, are considered fixed, and the data is random [40] [11].
• Reliability Estimation: Common techniques include Maximum Likelihood Estimation (MLE) for point estimates of parameters (e.g., failure rate λ in an exponential model) and confidence intervals to express uncertainty. For example, a 95% confidence interval for a sensor's Mean Time To Failure (MTTF) implies that if the same experiment were repeated numerous times, 95% of the calculated intervals would contain the true MTTF [11]. It is a common misconception to interpret this as a 95% probability that the true value lies within a specific, calculated interval [40] [38].
• Handling Conflict: In evidence theory, the classical Dempster's rule of combination can produce counter-intuitive results when fusing highly conflicting evidence from multiple sensors, a problem famously highlighted by Zadeh [37].

The Bayesian Paradigm and the Role of Priors

The Bayesian paradigm offers a fundamentally different approach by formally integrating existing knowledge with empirical data.

• Philosophical Basis: Probability is interpreted as a degree of belief. Parameters are random variables, and the goal is to quantify belief in their possible values given the observed data [39] [11]. This is achieved through Bayes' theorem: Posterior ∝ Likelihood × Prior.
• Specifying Prior Distributions: The prior distribution is the mechanism for incorporating existing knowledge.
  • Expert Elicitation: This is a structured interview process that guides domain experts to express their knowledge in probabilistic form. For instance, experts might be asked to bet on parameter values or assess the plausibility of future data to formulate an informed prior [41]. The reliability of a sensor can be assessed conditionally on different contexts (e.g., different target types or weather conditions), leading to a vector of discount rates rather than a single number [42].
  • Historical Data: Data from previous, similar systems or experiments can be used to construct an empirical prior. In hierarchical Bayesian modeling, this can be extended by placing hyperpriors on the parameters of the prior distribution itself, adding another layer of flexibility [43].
• Expressing Results: The outcome of a Bayesian analysis is the posterior distribution. Summaries of this distribution, such as the credible interval, provide an intuitive and direct probabilistic statement. A 95% credible interval means there is a 95% probability that the true parameter value lies within that interval, given the data and the prior [38] [39].

The following diagram illustrates the fundamental workflow of the Bayesian approach to updating beliefs about a sensor's reliability.

Comparative Experimental Analysis

To objectively compare the performance of classical and Bayesian methods, we outline a standardized experimental protocol and present synthesized results from the literature.

Experimental Protocol for Sensor Reliability Evaluation

• System Modeling: Define a target recognition system with a set of heterogeneous sensors (e.g., optical, RADAR, infrared) [36]. The frame of discernment, Ω, might consist of possible target classes {ω₁, ω₂, ..., ωₚ}.
• Data Generation: Simulate sensor outputs and true target classes. Data should include:
  • A training set for establishing baseline performance.
  • A test set with varying conditions (e.g., different targets, environmental noise) to evaluate dynamic performance [36].
• Reliability & BBA Determination:
  • Classical Method: Compute a static reliability factor for each sensor based on its confusion matrix or recognition rate from the training set. Generate Basic Belief Assignments (BBA) and combine them using Dempster's rule (potentially with pre-processing to handle conflict) [37].
  • Bayesian Method: Elicit prior distributions for sensor reliability from experts or derive them from the training set. For evidence theory, implement a discounting operation (classical or contextual) using the reliability factor α, where the BBA m is transformed to m_α [36] [42]. Update beliefs using Bayesian inference or the appropriate combination rule.
• Performance Metrics: Compare methods based on target classification accuracy, robustness to conflicting evidence, and computational efficiency.

Quantitative Comparison of Methodologies

The table below summarizes a synthesized comparison based on experimental results from the reviewed literature.

Table 1: Comparative performance of classical and Bayesian methods in sensor reliability analysis

Feature	Classical (Frequentist) Methods	Bayesian Methods
Philosophical Basis	Probability as long-run frequency [40]	Probability as degree of belief [39]
Treatment of Parameters	Fixed, unknown quantities [11]	Random variables with distributions [11]
Use of Prior Knowledge	Not directly incorporated	Formally incorporated via prior distributions [41]
Output Interpretation	Confidence Interval: Refers to long-run frequency of the method [38]	Credible Interval: Direct probability statement about the parameter [38]
Performance with Small Data	Can be unstable, high-variance estimates [11]	More stable and informative inferences [41] [11]
Handling Conflict	Dempster's rule can yield counter-intuitive results with high conflict [37]	Contextual discounting allows for refined, adaptive handling of conflict [36] [42]
Computational Complexity	Generally lower, more computationally efficient [11]	Higher, especially with MCMC and complex hierarchical models [43] [11]
Adaptability	Static reliability assessment requires explicit re-calibration	Self-adapting reliability through continuous updating of the posterior [36]

Table 2: Exemplary classification accuracy (%) under different conflict scenarios

Data Condition	Classical Dempster's Rule	Classical with Static Discounting	Bayesian with Contextual Discounting [42]
Low Conflict	94.5	95.1	95.8
High Conflict	62.3 (Counter-intuitive)	78.5	89.2
Dynamic Environment	70.1	81.4	92.6

The Researcher's Toolkit: Key Methods and Techniques

Table 3: Essential reagents and methodologies for sensor reliability research

Item	Function/Description	Application Context
Dempster-Shafer Theory	A framework for representing and combining evidence and uncertainty without requiring a prior probability [36] [37].	Multi-sensor data fusion, target classification.
Basic Belief Assignment (BBA)	A function (m) that assigns a belief mass to subsets of a frame of discernment, representing the evidence from a source [36] [37].	The foundational representation of evidence in D-S theory.
Discounting Operation	A technique to weaken a BBA based on the reliability (α) of its source. The classic Shafer discounting is m_α(A) = (1-α)*m(A) and m_α(Ω) = (1-α)*m(Ω) + α [36] [42].	Correcting sensor evidence before combination.
Contextual Discounting	An advanced discounting method parameterized by a vector of discount rates, representing the source's reliability in different contexts (e.g., different target types) [42].	Handling sensors with condition-dependent performance.
Pignistic Probability (BetP)	A probability transformation derived from a BBA, used for decision-making in the Transferable Belief Model [36] [37].	Making final decisions (e.g., target classification) from fused evidence.
Markov Chain Monte Carlo (MCMC)	A class of algorithms for sampling from complex probability distributions, fundamental to computational Bayesian inference [11].	Approximating posterior distributions in high-dimensional Bayesian models.
Normalizing Flows (NFs)	A technique using sequences of invertible mappings to transform simple probability distributions into complex ones, used for flexible reparameterization [43].	Decorrelating parameters in hierarchical Bayesian models to reduce prior sensitivity.
Grasshopper ketone	Grasshopper ketone, MF:C13H20O3, MW:224.30 g/mol	Chemical Reagent
Chikusetsusaponin Iva	Chikusetsusaponin IVa

Discussion and Synthesis of Results

The experimental data and theoretical examination reveal a clear, context-dependent trade-off between classical and Bayesian methods. The primary advantage of the Bayesian approach is its principled and flexible mechanism for incorporating expert opinion and historical data, which leads to more robust performance in the face of uncertainty. This is exemplified by its superior handling of high-conflict evidence and dynamic environments, as shown in Table 2. Methods like contextual discounting provide a refined way to model sensor reliability that is conditional on the context, moving beyond the simplistic single-reliability-factor model [36] [42]. This self-adapting capability is invaluable in real-world applications where sensor performance is not static.

However, this power comes with costs. Bayesian methods, particularly those employing MCMC or Hierarchical Models, are computationally more intensive than their classical counterparts [11]. Furthermore, the specification of the prior distribution introduces an element of subjectivity, which can be a source of controversy. Research shows that while interpersonal variation in elicited priors from different experts does affect Bayes factors, it does not always change the qualitative conclusion of a hypothesis test [41]. Sensitivity analysis is therefore a critical component of rigorous Bayesian practice.

Classical methods remain highly valuable. Their computational efficiency, objectivity, and well-understood asymptotic properties make them ideal for applications with abundant, high-quality data and where prior information is scarce or unreliable [11]. They provide a straightforward, standardized baseline against which more complex models can be evaluated. The following diagram synthesizes the decision-making process for selecting an appropriate methodology.

In the domain of sensor reliability analysis, the choice between classical and Bayesian methods is not a matter of which is universally superior, but which is most appropriate for the specific problem context. Classical frequentist methods provide an objective, computationally efficient framework well-suited to scenarios with ample data and minimal prior knowledge. In contrast, Bayesian methods excel in their ability to formally integrate expert opinion and historical data through prior distributions, offering more intuitive results and superior adaptability in dynamic, data-scarce, or high-conflict environments.

The emerging trend is not a strict dichotomy but a pragmatic integration. For instance, one can use classical methods on historical data to formulate an objective prior for a subsequent Bayesian analysis. Furthermore, advanced techniques like contextual discounting in belief function theory and parameter decorrelation using Normalizing Flows in hierarchical Bayesian models are pushing the boundaries of what is possible, enabling more robust, self-adapting, and reliable multi-sensor fusion systems [42] [43]. For researchers and engineers, the key is to understand the strengths and limitations of each paradigm and to apply them—singly or in combination—with a clear view of the operational requirements and constraints of their specific application.

Advanced Modeling with Bayesian Networks for Complex System Reliability

System reliability analysis is fundamental to ensuring the safety and performance of critical infrastructure and industrial systems. Traditional classical (frequentist) statistical methods have long dominated this field, relying on historical failure data and treating system parameters as fixed but unknown quantities. These approaches typically utilize Maximum Likelihood Estimation (MLE) and confidence intervals to draw inferences from observed data, emphasizing long-run frequency interpretations of probability [11]. While computationally efficient and widely implemented in industrial standards, classical methods face significant limitations when addressing modern engineering challenges characterized by multi-component dependencies, limited failure data, and evolving operational conditions.

In contrast, Bayesian networks (BNs) have emerged as a powerful probabilistic framework that explicitly represents uncertainty through graphical models. A Bayesian network is defined as an ordered pair N = (G, Θ) where G represents a directed acyclic graph (DAG) structure encoding variable dependencies, and Θ represents the network parameters defining conditional probability distributions [44]. This approach provides a fundamentally different philosophical foundation, treating unknown parameters as random variables with associated prior probability distributions that are updated with observational data through Bayes' theorem to form posterior distributions [6]. The Bayesian paradigm enables researchers to incorporate multiple information sources—including expert knowledge, simulation data, and sparse experimental observations—into a unified probabilistic reasoning framework particularly suited for complex system reliability assessment under uncertainty [45] [46].

This comparison guide examines the theoretical foundations, methodological approaches, and practical applications of both classical and Bayesian methods for reliability analysis, with particular emphasis on complex systems where multiple component interactions and uncertain operating conditions complicate traditional assessment approaches.

Theoretical Foundations and Methodological Comparison

Fundamental Differences in Probability Interpretation

The philosophical divide between classical and Bayesian reliability methods originates from their contrasting interpretations of probability. Classical statistics defines probability as the long-run frequency of an event occurrence. For fixed but unknown parameters such as a failure rate (λ), classical methods consider the parameter as deterministic, leading to binary probability statements about whether the parameter lies within a specific interval [6]. This perspective underpins commonly used classical reliability techniques including Non-Homogeneous Poisson Processes (NHPP) for repairable systems with time-varying failure rates, Weibull analysis for lifetime distributions, and the Kaplan-Meier estimator for survival analysis with censored data [11].

Bayesian statistics fundamentally redefines probability as quantified belief in a statement's truth. This epistemic interpretation enables probabilistic statements about parameters themselves, such as expressing the probability that a system's reliability exceeds 0.95 as 90% [6]. Bayesian methods achieve this through a consistent mathematical framework for updating prior beliefs with empirical evidence. Formally, this process follows Bayes' rule:

[ \pi(\theta \mid \mathbf{x}) = \frac{p(\mathbf{x} \mid \theta) \pi(\theta)}{\int_{\Theta} p(\mathbf{x} \mid \theta) \pi(\theta)\, d\theta} \propto p(\mathbf{x} \mid \theta) \pi(\theta) ]

where (\pi(\theta)) represents the prior distribution encapsulating initial beliefs about parameter θ, (p(\mathbf{x} \mid \theta)) is the likelihood function of observed data (\mathbf{x}), and (\pi(\theta \mid \mathbf{x})) is the posterior distribution representing updated beliefs after considering the evidence [6].

Comparative Strengths and Limitations

Table 1: Methodological Comparison Between Classical and Bayesian Reliability Approaches

Aspect	Classical Methods	Bayesian Networks
Probability Interpretation	Long-run frequency of events	Degree of belief in statements
Parameter Treatment	Fixed but unknown quantities	Random variables with distributions
Prior Knowledge Incorporation	Not directly supported	Explicitly integrated via prior distributions
Uncertainty Quantification	Confidence intervals based on hypothetical repeated sampling	Posterior credible intervals with direct probability interpretation
Computational Demands	Generally lower; closed-form solutions often available	Generally higher; often requires Markov Chain Monte Carlo (MCMC) sampling
Small-Sample Performance	Potentially unreliable with limited data	More robust through informative priors
Complex System Modeling	Limited to simpler dependencies	Excellent for multi-component, causal relationships
Results Interpretation	Indirect (confidence level refers to method, not parameter)	Direct (credible interval contains parameter with specific probability)
Data Requirements	Requires substantial failure data for accuracy	Effective with limited data when priors are informative

Bayesian networks extend core Bayesian principles to complex system modeling by representing causal relationships between components and subsystems through directed graphical structures. The network topology consists of nodes (representing system variables) connected by directed edges (representing probabilistic dependencies). Each node associates with a conditional probability table (CPT) or conditional probability distribution (CPD) that quantitatively defines relationships with parent nodes [44] [45]. This graphical representation enables intuitive modeling of complex, multi-component systems where reliability emerges from component interactions rather than isolated component performances.

For reliability assessment, Bayesian networks provide multiple distinctive advantages: (1) visualization of causal pathways through which component failures propagate to system-level effects; (2) efficient probabilistic inference using exact algorithms such as the Junction Tree (JT) algorithm or approximate sampling methods; and (3) bi-directional reasoning capabilities supporting both predictive analysis (from causes to effects) and diagnostic analysis (from effects to causes) [47] [45]. The Junction Tree algorithm specifically enhances computational efficiency by clustering network nodes, enabling exact inference in complex networks through systematic message passing between clusters [47].

Experimental Protocols and Implementation Frameworks

Bayesian Network Development Methodology

Implementing Bayesian networks for reliability analysis follows a systematic methodology encompassing model construction, parameter learning, and probabilistic inference. The following diagram illustrates the comprehensive workflow for Bayesian network-based reliability assessment:

The Bayesian network reliability assessment workflow follows a systematic four-stage process encompassing problem formulation, model construction, validation, and reliability analysis, with iterative feedback loops enabling continuous model refinement.

Phase 1: Problem Formulation and System Decomposition The initial phase involves comprehensive system analysis to identify critical components, failure modes, and functional dependencies. For a mining truck reliability analysis [48], this includes decomposing the system into major subsystems (engine, transmission, hydraulic systems, etc.), defining performance states for each component (operational, degraded, failed), and establishing system-level reliability metrics (e.g., probability of mission completion, mean time between failures). This stage typically leverages Failure Mode and Effects Analysis (FMEA) and fault tree analysis to systematically identify potential failure pathways and their system-level consequences.

Phase 2: Network Structure Development and Parameter Estimation Based on the system decomposition, the BN structure is constructed by representing components as nodes and their functional dependencies as directed edges. In the mining truck application [48], the resulting network represented relationships between 20+ components across major subsystems. Conditional probability distributions are then specified for each node based on either historical failure data, expert judgment, or laboratory testing results. For components with limited historical data, Bayesian parameter estimation techniques leverage conjugate prior distributions (e.g., Beta distribution for failure probabilities) to derive posterior distributions that incorporate both prior knowledge and sparse observational data [6].

Phase 3: Model Validation and Sensitivity Analysis The constructed BN model undergoes rigorous validation through multiple approaches: (1) sensitivity analysis identifies parameters with greatest influence on system reliability predictions; (2) historical data validation compares model predictions with actual failure records; and (3) expert review ensures causal relationships accurately reflect engineering principles. In structural health monitoring applications [44], BN models are typically validated using sensor data from known structural states to quantify model accuracy and refine conditional probability specifications.

Phase 4: Reliability Analysis and Inference The validated BN model supports diverse reliability analysis tasks through probabilistic inference algorithms. Key applications include: (1) predictive analysis estimating system reliability given specific operational conditions; (2) diagnostic reasoning identifying most probable root causes given observed failure symptoms; and (3) criticality analysis quantifying contributions of individual components to system failure probability. For dynamic systems, Dynamic Bayesian Networks (DBNs) extend the standard framework to explicitly model temporal evolution of component states and reliability metrics [49].

Classical Reliability Assessment Protocols

Classical reliability assessment methodologies follow fundamentally different experimental protocols centered on statistical estimation from failure data. The standard approach involves:

Data Collection and Lifetime Distribution Modeling Classical methods begin with collecting time-to-failure data or time-between-failure data from historical records or accelerated life testing. Statistical techniques then fit parametric lifetime distributions (e.g., Weibull, lognormal, exponential) to the observed failure data using Maximum Likelihood Estimation (MLE). For the mining truck reliability analysis [48], this involved collecting 3+ years of maintenance records and fitting Weibull distributions to subsystem failure data. The resulting distribution parameters (e.g., shape and scale parameters for Weibull distribution) provide the basis for reliability quantification.

System Reliability Modeling For multi-component systems, classical approaches typically employ reliability block diagrams (RBDs) to model system configuration and derive mathematical reliability functions. Series systems reliability is computed as the product of component reliabilities ( Rs(t) = \prod{i=1}^{n} Ri(t) ), while parallel systems use ( Rp(t) = 1 - \prod{i=1}^{n} [1 - Ri(t)] ) [11]. These simplified mathematical models struggle to capture complex component interactions and causal relationships that Bayesian networks explicitly represent.

Confidence Interval Estimation Classical methods quantify estimation uncertainty through confidence intervals derived from the sampling distribution of reliability estimates. For the Type II censored lognormal distribution analysis [4], classical approaches computed confidence bounds based on asymptotic normal approximations of parameter sampling distributions. This provides a frequentist interpretation where a 95% confidence interval would contain the true reliability parameter in 95% of hypothetical repeated experiments.

Comparative Performance Analysis: Experimental Evidence

Quantitative Performance Metrics Across Applications

Empirical studies across diverse engineering domains provide quantitative evidence comparing classical and Bayesian reliability assessment performance. The following table synthesizes key findings from multiple case studies implementing both methodologies:

Table 2: Experimental Performance Comparison Across Engineering Applications

Application Domain	Classical Method	Bayesian Network Approach	Key Performance Findings
Mining Truck Fleet Reliability [48]	Weibull analysis of subsystem failure data	Dynamic BN with 20+ component nodes	BN identified fuel injection system as most critical (28% contribution to failures) versus classical ranking of suspension system; BN fleet reliability prediction at 20h: 0.881 with diagnostic reasoning capabilities
CVT Online Monitoring [46]	Physical model-based reliability prediction	BN with environmental and component nodes	BN accuracy: 92.3% in fault detection versus 76.5% for physical models; BN identified high-temperature+high-humidity as most critical condition (95% failure probability)
Aircraft System (k-out-of-N) [47]	Direct integration method	BN with Junction Tree algorithm	Computational efficiency: BN+JT handled N=100 components with 5 types versus classical methods limited to N<50; BN enabled hybrid (continuous+discrete) inference unavailable in classical approach
Structural Health Monitoring [44]	Traditional sensor threshold alarms	BN with multi-sensor data fusion	BN reduced false alarms by 67% while maintaining 98% detection sensitivity; BN enabled damage quantification with 89% accuracy versus binary detection only in classical approach
Power Equipment [45]	First Order Second Moment (FOSM) method	BN with dynamic updating	BN reliability predictions updated in real-time with new inspection data; 20-30% improvement in maintenance planning accuracy compared to classical static reliability estimates

The experimental evidence consistently demonstrates Bayesian networks' superior performance in modeling complex system reliability, particularly in scenarios involving multiple dependent components, uncertain operating conditions, and limited failure data. Across applications, BNs provide not only comparable or improved reliability predictions but also enhanced diagnostic capabilities and root cause analysis unavailable through classical methods.

Small-Sample Performance and Prior Sensitivity

The comparative performance between classical and Bayesian methods becomes particularly pronounced in small-sample scenarios common to high-reliability systems. Experimental analysis of failure-censored sampling for lognormal lifetime distributions [4] demonstrated that Bayesian methods maintain stable risk predictions (producer's risk < 0.05, consumer's risk < 0.10) with sample sizes 30-50% smaller than classical methods requiring equivalent risk control. This advantage derives from Bayesian methods' ability to incorporate prior information through formal probability distributions.

The following diagram illustrates how Bayesian networks integrate multiple information sources and enable both predictive and diagnostic reasoning for reliability assessment:

Bayesian networks integrate multiple information sources including expert knowledge, historical data, sensor measurements, and laboratory testing to enable comprehensive reliability assessment with both predictive and diagnostic capabilities.

Sensitivity to prior distribution specification represents a fundamental consideration in Bayesian reliability analysis. Experimental investigations [6] [4] demonstrate that prior distribution influence diminishes as observational data increases, with posterior distributions dominated by likelihood functions when sample sizes exceed 20-30 failures. For high-reliability systems with sparse failure data, hierarchical Bayesian models and empirical Bayes methods provide robust approaches for prior specification, while sensitivity analysis techniques quantify how prior assumptions affect final reliability conclusions.

Methodological Framework Comparison

Table 3: Essential Methodological Toolkit for Reliability Assessment

Method Category	Specific Techniques	Primary Function	Applicability Conditions
Classical Methods	Maximum Likelihood Estimation (MLE)	Parameter estimation for lifetime distributions	Substantial failure data available (>30 failures)
	Reliability Block Diagrams (RBD)	System-level reliability modeling	Systems with simple series/parallel configurations
	Fault Tree Analysis (FTA)	Deductive failure analysis	Identifying system failure root causes
	Weibull Analysis	Lifetime distribution modeling	Time-to-failure data with trendable hazard rates
Bayesian Methods	Bayesian Parameter Estimation	Prior knowledge integration with data	Limited data or informative prior knowledge available
	Markov Chain Monte Carlo (MCMC)	Posterior distribution computation	Complex models without analytical solutions
	Junction Tree Algorithm	Exact inference in Bayesian networks	Discrete networks or conditional Gaussian models
	Dynamic Bayesian Networks (DBNs)	Temporal reliability modeling	Systems with time-dependent failure processes
	Sensitivity Analysis	Prior distribution impact assessment	Quantifying robustness of reliability conclusions
Cross-Paradigm	First Order Reliability Method (FORM)	Component reliability approximation	Performance functions with known limit states
	Subset Simulation	Small failure probability estimation	System reliability with rare failure events

Successful implementation of Bayesian networks for reliability analysis requires both methodological expertise and computational tools. The BNS-JT toolkit (MATLAB-based) provides specialized functionality for system reliability analysis using the Junction Tree algorithm, specifically designed to handle the computational complexity of large-scale systems [47]. General-purpose Bayesian network software including BayesFusion, HUGIN, and OpenBUGS offer graphical interfaces for model development and multiple inference algorithms.

For classical reliability assessment, established tools such as Weibull++, Reliability Block Diagram Software, and statistical packages including R and SAS provide comprehensive functionality for lifetime data analysis and system reliability modeling. The emerging trend toward hybrid approaches leverages strengths of both paradigms, using classical methods for component-level reliability estimation and Bayesian networks for system-level integration and uncertainty propagation [11] [45].

Computational requirements represent a significant practical consideration, with Bayesian network inference complexity growing with network connectivity and node states. The Junction Tree algorithm mitigates this challenge through systematic clustering and message passing, enabling exact inference in complex networks with hundreds of nodes [47]. For particularly large-scale systems, approximate inference algorithms including loopy belief propagation and Markov Chain Monte Carlo (MCMC) sampling provide practical alternatives with demonstrated success in reliability applications [48] [46].

The comparative analysis demonstrates that both classical and Bayesian reliability methods offer distinct advantages suited to different application contexts. Classical methods provide computationally efficient, well-established approaches for systems with substantial failure data, simple component interactions, and contexts where prior knowledge incorporation is undesirable. Their straightforward interpretation and extensive standardization make them appropriate for component-level reliability analysis and regulatory compliance contexts.

Bayesian networks excel in complex system reliability assessment where multiple information sources must be integrated, component dependencies significantly influence system behavior, and diagnostic reasoning capabilities provide operational value. The ability to formally quantify and update uncertainty through Bayesian learning makes this approach particularly valuable for systems with limited historical data, evolving operational conditions, and requirements for real-time reliability assessment.

For researchers and practitioners, method selection should consider multiple factors: (1) data availability - classical methods require substantial failure data while Bayesian approaches effectively leverage prior knowledge; (2) system complexity - Bayesian networks better capture complex component interactions; (3) analysis objectives - Bayesian networks support both predictive and diagnostic reasoning; and (4) computational resources - classical methods generally have lower computational requirements. The emerging methodology of hybrid approaches that leverage strengths of both paradigms represents a promising direction for advancing complex system reliability assessment, potentially offering robust solutions that balance computational efficiency with modeling flexibility and comprehensive uncertainty quantification.

Reliability analysis is fundamental to validating wearable healthcare sensors before their data can be trusted for clinical research or patient care. Two dominant statistical paradigms exist for this analysis: the classical (frequentist) approach, which relies solely on observed data from controlled experiments, and the Bayesian approach, which incorporates prior knowledge or expert belief to update beliefs about a sensor's reliability [11]. This case study investigates the application of both methods for evaluating the reliability of a specific wearable sensor, the Xsens DOT, a commercially available Inertial Measurement Unit (IMU) [50]. The objective is to objectively compare its performance against a gold-standard system and delineate the practical implications of choosing a classical versus Bayesian framework for reliability assessment. This comparison is crucial for researchers and drug development professionals who rely on sensor-derived digital endpoints, as the choice of statistical method can significantly influence the interpretation of a device's performance and the subsequent decisions based on its data.

Methodological Frameworks

Classical (Frequentist) Reliability Analysis

Classical methods treat reliability parameters as fixed, unknown values to be estimated solely from empirical data [11]. This framework employs hypothesis testing and confidence intervals to quantify measurement precision.

• Core Principle: Parameters, such as a sensor's mean error, are fixed. Probability is interpreted as the long-run frequency of an event over repeated trials [6].
• Common Techniques:
  • Maximum Likelihood Estimation (MLE): Used for parameter estimation in lifetime distributions like the Weibull model [11].
  • Intraclass Correlation Coefficient (ICC): Measures consistency or agreement between measurements. ICC values range from 0 to 1, with higher values indicating better reliability [50].
  • Bland-Altman Plots: Visualize agreement between two measurement techniques by plotting differences against averages, establishing limits of agreement [50].
  • Linear Fit Method (LFM): Assesses concurrent validity by comparing signal waveforms from a test sensor and a gold-standard criterion [50].

Bayesian Reliability Analysis

Bayesian methods treat reliability parameters as random variables with probability distributions, formally incorporating prior knowledge or expert opinion through Bayes' theorem [6] [11].

• Core Principle: Probability quantifies a degree of belief. Prior beliefs about a parameter are updated with observed data to form a posterior distribution [6].
• The Bayesian Engine: The process is governed by Bayes' theorem: Posterior ∝ Likelihood × Prior [6]. This framework is particularly advantageous in small-sample contexts or when integrating data from computer simulations and expert judgment [11].
• Key Advantage: It provides a direct probabilistic interpretation of reliability, such as "the probability that the sensor's reliability exceeds 0.95 is 90%," which is a more intuitive and informative result for decision-making than a classical confidence interval [6].

Table: Core Differences Between Classical and Bayesian Reliability Analysis

Feature	Classical (Frequentist) Approach	Bayesian Approach
Parameter Nature	Fixed, unknown constant	Random variable with a distribution
Probability Definition	Long-run frequency	Degree of belief
Prior Knowledge	Not formally incorporated	Formally incorporated via prior distributions
Output	Point estimate and confidence interval	Full posterior distribution
Interpretation	Confidence interval: range over repeated experiments	Credible interval: direct probability statement about the parameter
Computational Complexity	Often lower; closed-form solutions	Often higher; relies on simulation (e.g., MCMC)

Experimental Protocol for Sensor Validation

To generate data for a reliability analysis, a robust experimental protocol must be implemented. The following methodology, adapted from a study on the Xsens DOT sensor, provides a template for such validation [50].

Sensors and Equipment

• Test Sensor: The device under evaluation, e.g., the Xsens DOT IMU.
• Criterion (Gold-Standard) Sensor: An already-validated system used as a benchmark, e.g., the Xsens MTw Awinda system [50].
• Synchronization System: To ensure data from both systems are temporally aligned.

Participant Recruitment

• A sample of healthy adults (e.g., n=21), with data collected on demographic characteristics like age, BMI, and limb dominance [50].

Data Collection Procedure

The experiment involves three distinct sessions conducted in a single day to assess both validity and reliability [50]:

• Session 1 (Researcher-Attached): A researcher attaches both the test and criterion sensors to the participant's body segments (e.g., sacrum, thigh, shank).
• Session 2 (Researcher-Attached, Retest): After a short break, the researcher re-attaches all sensors to assess test-retest reliability.
• Session 3 (Participant-Attached): The participant attaches the sensors themselves to simulate real-world usage.

During each session, participants perform a series of functional activities to challenge the sensors across different movement patterns:

• Walking
• Stair ambulation
• Squats
• Jumping [50]

This multi-activity, multi-session design is critical for evaluating the sensor's performance across varied, ecologically valid contexts [51].

Data Analysis Methods

The collected data is analyzed to extract key metrics, such as the range of accelerations and orientations for each activity. These metrics are then used in the statistical analyses described in Section 2 [50].

The workflow below illustrates the parallel processes of classical and Bayesian analysis stemming from a common experimental protocol.

Results & Data Analysis

Quantitative Performance Comparison

The data obtained from the validation study provides concrete metrics for evaluating the Xsens DOT sensor. The following tables summarize key findings for acceleration and orientation measurements, comparing the sensor's performance across different attachment conditions and activities [50].

Table 1: Test-Retest Reliability of Acceleration Measurements (ICC Values)

Body Segment	Activity	Researcher-Attached (Session 1 vs 2)	Participant-Attached (Session 1 vs 3)
Sacrum	Walking	0.92 (Excellent)	0.85 (Good)
Thigh	Squats	0.88 (Good)	0.79 (Fair)
Shank	Stair Ambulation	0.95 (Excellent)	0.82 (Good)
Thigh	Jumping	0.75 (Fair)	0.65 (Fair)

Table 2: Concurrent Validity of Orientation Measurements (LFM r² Values)

Body Segment	Activity	r² Value (Vs. Gold Standard)	Validity Interpretation
Sacrum	Walking	0.94	Excellent
Shank	Squats	0.89	Good
Thigh	Stair Ambulation	0.91	Excellent
Shank	All Activities (Z-axis)	0.45 - 0.60	Fair to Poor

Classical vs. Bayesian Analysis of Reliability Data

Consider a scenario where the Xsens DOT sensor is tested for its ability to accurately classify a specific posture (e.g., a squat) over a series of n=100 trials. It successfully classifies x=95 squats.

• Classical Analysis: Using Maximum Likelihood Estimation, the point estimate for reliability is 95/100 = 0.95. A 95% confidence interval might be calculated as (0.89, 0.98). This means that if we were to repeat this experiment many times, 95% of such calculated intervals would contain the true, fixed reliability parameter [11].
• Bayesian Analysis: A Bayesian would start with a prior distribution for reliability. If no strong prior knowledge exists, a non-informative Beta(1,1) (Uniform) prior could be used. With x=95 successes in n=100 trials, the posterior distribution is a Beta(95+1, 5+1) = Beta(96,6). From this distribution, one can directly state that the probability that reliability exceeds 0.90 is over 99%, or calculate a 95% credible interval, such as (0.90, 0.98) [6]. This interval has a direct interpretation: there is a 95% probability that the true reliability lies between 0.90 and 0.98, given the data and the prior.

This case demonstrates that while both methods might yield similar numerical intervals in some cases, their interpretations are fundamentally different. The Bayesian approach is particularly useful when test trials are limited (n is small), as it allows for the formal incorporation of prior information from simulations or expert opinion to produce a more precise estimate [6] [11].

The Scientist's Toolkit

The following reagents, materials, and software are essential for conducting a comprehensive reliability analysis of wearable sensors.

Table 3: Essential Research Reagents and Materials for Sensor Reliability Studies

Item	Function / Purpose	Example
Research-Grade IMU	The device under test; measures acceleration, orientation, and other movement metrics.	Xsens DOT [50]
Gold-Standard Motion System	Provides criterion measure for validating the test sensor's outputs.	Xsens MTw Awinda, VICON motion capture [50]
Beta Distribution	A flexible family of continuous distributions on (0,1) used as a conjugate prior for reliability/probability parameters in Bayesian analysis.	Used to model the prior and posterior distribution of a sensor's success rate [6]
Statistical Software	For performing both classical (ICC, Bland-Altman) and Bayesian (MCMC) analyses.	R, Python (with PyMC, Stan), JAGS [11]
Data Synchronization Tool	Hardware or software solution to temporally align data streams from different sensors for valid comparison.	Sync, trigger boxes, or post-hoc alignment algorithms [50]
Telekin	Telekin, MF:C15H20O3, MW:248.32 g/mol	Chemical Reagent
Arjunic acid	Arjunic acid, MF:C30H48O5, MW:488.7 g/mol	Chemical Reagent

This case study demonstrates a complete framework for analyzing the reliability of a wearable healthcare sensor, using the Xsens DOT as a model. The experimental data shows that while the sensor generally provides valid and reliable measures of acceleration and orientation, its performance is context-dependent, varying with the type of activity and who attaches the sensor [50].

The comparison between classical and Bayesian methods reveals a fundamental trade-off. Classical methods offer objectivity, computational simplicity, and are well-suited for initial validation with sufficient data. In contrast, Bayesian methods provide a more flexible and intuitive inference engine, capable of formally integrating diverse sources of knowledge and providing direct probability statements about reliability, which is invaluable for decision-making with limited data [6] [11].

For researchers in healthcare and drug development, the choice is not about which method is universally superior, but about selecting the right tool for the question at hand. A hybrid approach is often most powerful: using classical methods for initial, standardized validation reporting, and leveraging Bayesian analysis for refining reliability estimates, designing more efficient trials, and making predictions about sensor performance in real-world, heterogeneous patient populations.

Utilizing Frequency Response Function (FRF) Data for Model Updating

Model updating is a critical process in structural dynamics for ensuring computational models accurately reflect real-world behavior. This guide compares the performance of classical deterministic and modern Bayesian methodologies for model updating using Frequency Response Function (FRF) data, providing a structured analysis for researchers in sensor reliability and system identification.

Experimental Protocols & Methodologies

The following section details the standard experimental and computational workflows for the primary methodologies discussed in this review.

Workflow for FRF-Based Model Updating

The following diagram illustrates the general workflow for FRF-based model updating, highlighting the parallel paths for classical and Bayesian methodologies.

Core Methodological Protocols

1. Classical Semi-Direct Finite Element Updating [52] This hybrid approach combines iterative and direct updating techniques:

• Step 1 - Iterative Model Updating: Conventional sensitivity-based updating is performed to match analytical and experimental eigenfrequencies and mode shapes within 3-5% tolerance limits.
• Step 2 - Direct Matrix Updating: Eigenfrequency deviations are eliminated by replacing analytical values with measured ones without changing corresponding eigenvectors. The stiffness matrix is recalculated using a matrix-mixing approach while preserving the mass matrix.
• Step 3 - Damping Refinement: Unmeasured modal damping ratios are obtained by minimizing the FRF error function, significantly improving FRF correlation with test data.

2. Traditional Bayesian Framework with MCMC Sampling [53] [54] This probabilistic approach incorporates parameter uncertainties:

• Step 1 - Prior Definition: Establish prior probability distributions for uncertain model parameters based on physical constraints or engineering judgment.
• Step 2 - Likelihood Formulation: Construct a likelihood function, typically multivariate Gaussian, that quantifies the discrepancy between experimental and analytical FRFs.
• Step 3 - Posterior Computation: Employ Markov Chain Monte Carlo (MCMC) sampling methods, such as the Metropolis algorithm or transitional MCMC, to generate samples from the posterior distribution of parameters given the observed FRF data.

3. Advanced Hierarchical Bayesian Modeling (HBM) [55] [56] [57] This sophisticated extension addresses multiple uncertainty sources:

• Step 1 - Multi-Level Structure: Implement a hierarchical structure with population-level (hyper-) parameters and domain-level parameters, enabling information sharing among similar structures or multiple datasets.
• Step 2 - Probabilistic FRF Modeling: Incorporate complex-valued FRF data using Gaussian likelihood formulations that capture both magnitude and phase information (real and imaginary parts).
• Step 3 - Analytical Inference: Utilize variational inference techniques to derive analytical solutions for posterior distributions, significantly improving computational efficiency compared to sampling-based methods.

Quantitative Performance Comparison

The table below summarizes key performance metrics for each methodology based on experimental implementations documented in the literature.

Methodology	Parameter Estimation Accuracy	Uncertainty Quantification	Computational Efficiency	Implementation Complexity	Key Advantages
Classical Semi-Direct [52]	High point estimates	Limited	High	Moderate	Excellent FRF correlation; Preserves physical meaning
Traditional Bayesian [53] [58]	Moderate with variance	Comprehensive but may be underestimated	Low (sampling-intensive)	High	Rigorous uncertainty treatment; Handles various errors
Hierarchical Bayesian (HBM) [57]	High with population trends	Comprehensive multiple uncertainty sources	Moderate with analytical solutions	Very High	Information sharing; Conservative reliability estimates

The Researcher's Toolkit: Essential Computational Methods

Method/Technique	Function in FRF-Based Updating	Key References
Markov Chain Monte Carlo (MCMC)	Samples from posterior parameter distributions	[53] [54]
Polynomial Chaos Expansion (PCE)	Surrogate modeling for uncertainty propagation	[53]
Normalized Half-Power Bandwidth Frequency Transformation (NHBFT)	Preprocesses FRF data to conform to normality assumptions	[58]
Principal Component Analysis (PCA)	Reduces dimensionality of FRF data	[58] [59]
Variational Inference (VI)	Enables analytical solutions in hierarchical Bayesian models	[57]
Frequency Domain Assurance Criterion (FDAC)	Quantifies correlation between FRFs	[58]
Wilforol A	Wilforol A	Wilforol A is a pentacyclic triterpenoid from Tripterygium wilfordii for research applications. This product is for Research Use Only (RUO). Not for human or veterinary diagnostic or therapeutic use.
Tetrahydroauroglaucin	Tetrahydroauroglaucin, CAS:40434-07-9, MF:C19H26O3, MW:302.4 g/mol	Chemical Reagent

Key Methodological Insights

Relationship Between Updating Approaches

The diagram below shows how the various methodological approaches relate to each other and their key characteristics.

Classical deterministic methods provide efficient point estimates of parameters with high accuracy in matching FRF data [52]. The semi-direct approach excels in practical engineering applications where computational efficiency is prioritized and comprehensive uncertainty quantification is secondary. The method's strength lies in its systematic elimination of eigenfrequency error and refinement of damping parameters, producing excellent FRF correlation with test data.

Traditional Bayesian methods offer rigorous uncertainty quantification but face computational challenges [53]. These approaches naturally handle measurement noise, modeling errors, and parameter uncertainties within a unified probabilistic framework. The implementation typically requires sophisticated sampling algorithms like MCMC, which may involve thousands of model evaluations, making them computationally intensive for complex finite element models.

Advanced Bayesian approaches address limitations of traditional methods through methodological innovations [58] [57]. The integration of NHBFT-PCA metrics enables better handling of the complex, nonlinear relationship between parameters and FRFs near resonance peaks. Hierarchical Bayesian modeling provides superior uncertainty quantification for population-based studies and multiple dataset scenarios, correctly accounting for variability between datasets that classical Bayesian methods often underestimate [57].

The selection between classical and Bayesian methodologies for FRF-based model updating involves fundamental trade-offs between computational efficiency and uncertainty quantification. Classical approaches, particularly the semi-direct method, provide excellent FRF correlation with high computational efficiency, making them suitable for applications requiring rapid parameter estimation with limited concern for uncertainty bounds. In contrast, Bayesian methods offer comprehensive uncertainty quantification essential for reliability analysis and risk-informed decision making, despite their higher computational demands. For modern applications involving population-based structural health monitoring or multiple experimental datasets, hierarchical Bayesian models represent the most advanced approach, enabling information sharing while properly accounting for multiple uncertainty sources. The emerging trend of incorporating machine learning techniques with Bayesian inference promises to further enhance the efficiency and applicability of probabilistic FRF-based model updating in complex engineering systems.

Overcoming Challenges: Handling Sparse Data and Computational Complexity

Addressing the 'No-Failures' Problem with Bayesian Prior Information

In reliability engineering for critical systems, a fundamental paradox often arises: how to statistically demonstrate high reliability when testing reveals zero failures. This "no-failures" problem presents significant challenges for classical statistical methods, which struggle to quantify uncertainty with limited failure data. In fields ranging from aerospace systems to medical devices and sensor technologies, destructive testing, cost constraints, and high-reliability requirements naturally lead to sparse failure data [12] [6]. Classical frequentist approaches typically require implausibly large sample sizes to demonstrate high reliability with confidence when no failures occur during testing [60].

Bayesian statistics transforms this paradigm by formally incorporating prior knowledge through probability distributions, enabling more informative reliability assessments even with zero observed failures. This approach combines existing information—from expert judgment, historical data, simulations, or component testing—with limited new test results to form updated posterior distributions that reflect total available knowledge about system reliability [6] [11]. For reliability professionals working with high-cost systems like satellites, medical devices, or sophisticated sensors, this Bayesian framework provides a mathematically rigorous solution to the no-failures dilemma that classical methods cannot adequately address.

Theoretical Foundations: Classical versus Bayesian Approaches

Fundamental Differences in Statistical Philosophy

The classical and Bayesian statistical paradigms differ fundamentally in their interpretation of probability and treatment of unknown parameters, leading to distinct approaches for reliability demonstration:

Table 1: Fundamental Differences Between Classical and Bayesian Reliability Approaches

Aspect	Classical (Frequentist) Approach	Bayesian Approach
Probability Definition	Long-run frequency of events	Degree of belief in propositions
Parameter Treatment	Fixed but unknown quantities	Random variables with distributions
Primary Focus	Likelihood of observed data	Posterior distribution of parameters
Information Synthesis	Uses only current test data	Combines prior knowledge with new data
Uncertainty Quantification	Confidence intervals	Credible intervals
Zero-Failure Handling	Problematic; conservative estimates	Naturally incorporates prior information

Classical methods treat reliability parameters as fixed but unknown constants, attempting to estimate them solely from observed test data. With zero failures, these methods produce extremely conservative reliability estimates or require impractical sample sizes [11]. As noted in reliability engineering literature, "With no failures, it is difficult for classical statistics to accurately quantify the probability of failure" [6].

The Bayesian framework reinterprets probability as quantified belief, allowing reliability parameters to be represented as probability distributions that evolve as new information becomes available. This philosophical shift enables engineers to incorporate relevant prior information through carefully specified prior distributions, creating a more realistic and practical approach to reliability demonstration with limited data [6] [60].

Mathematical Formulation of the Bayesian Approach

The Bayesian reliability framework centers on Bayes' theorem, which provides a mathematically rigorous mechanism for updating beliefs about reliability parameters. For a reliability parameter θ (typically representing probability of success or failure rate), the posterior distribution after observing test data x is calculated as:

[ \pi(\theta \mid \mathbf{x}) = \frac{p(\mathbf{x} \mid \theta) \pi(\theta)}{\int_{\Theta} p(\mathbf{x} \mid \theta) \pi(\theta)\, d\theta} \propto p(\mathbf{x} \mid \theta) \pi(\theta) ]

where (\pi(\theta)) represents the prior distribution encoding previous knowledge about θ, (p(\mathbf{x} \mid \theta)) is the likelihood function representing the current test data, and (\pi(\theta \mid \mathbf{x})) is the posterior distribution representing the updated belief about θ after considering both sources of information [6].

For binomial success/failure data with zero failures in n tests, the likelihood function simplifies to (p(x \mid \theta) = \theta^n). When combined with a Beta(α, β) prior distribution—a conjugate prior for binomial sampling—the resulting posterior distribution is Beta(α + n, β), providing a closed-form solution that facilitates straightforward computation and interpretation [6] [60].

Figure 1: Bayesian inference workflow for reliability analysis, showing how prior knowledge and test data combine to form posterior distributions for reliability inference.

Methodological Comparison: Experimental Protocols and Applications

Bayesian Experimental Design for Zero-Failure Testing

Bayesian reliability demonstration tests are specifically designed to determine the minimum number of zero-failure tests needed to establish a required reliability level at a specified confidence. The experimental protocol involves:

• Define Reliability Requirement: Establish the required reliability level R (probability of success) and confidence level C (probability that R is achieved) [60].

• Specify Prior Distribution: Select an appropriate prior distribution for the success probability θ. For complete prior ignorance, use Beta(1,1) (uniform distribution). For informed priors, use Beta(α,β) with parameters based on historical data, expert judgment, or component testing [6].

• Calculate Test Sample Size: Determine the minimum number n of zero-failure tests needed such that the posterior probability P(θ ≥ R | n successes) ≥ C. For Beta(α,β) prior, this requires finding smallest n such that:

  [ P(\theta \geq R | n \text{ successes}) = \frac{\intR^1 \theta^{\alpha + n - 1}(1-\theta)^{\beta-1} d\theta}{\int0^1 \theta^{\alpha + n - 1}(1-\theta)^{\beta-1} d\theta} \geq C ]

  [60]

• Execute Testing Protocol: Conduct n tests under representative conditions, ensuring strict quality control to maintain test validity.

• Analyze Results: If all tests are successful, calculate the posterior reliability distribution. If failures occur, revise the design and repeat testing [60].

This methodology has been successfully applied across industries, from aerospace systems to mining equipment, demonstrating its versatility for high-reliability demonstration [12] [48].

Application Case Studies Across Industries

Table 2: Bayesian Reliability Applications Across Industries with Zero-Failure Testing

Industry	Application	Bayesian Method	Key Findings
Aerospace	Mission reliability prediction for missile systems [12]	Hierarchical Bayesian fusion of multi-fidelity test data	Significantly improved prediction accuracy with sparse physical test data
Mining	Reliability analysis of haul truck fleets [48]	Bayesian networks with fault tree integration	Identified fuel injection system as primary failure cause; achieved 0.881 fleet reliability at 20h
Optoelectronics	Reliability evaluation of satellite attitude sensors [61]	Wiener process degradation modeling with Bayesian updating	Effectively combined in-orbit data with ground tests for improved confidence
Rail Transport	Preventive maintenance of locomotive wheel-sets [5]	Bayesian semi-parametric degradation modeling	Supported optimal maintenance decisions combining classical and Bayesian results
Medical Devices	Reliability demonstration for safety-critical devices [6]	Beta-binomial model with informed priors	Enabled reliability quantification with limited clinical testing

The Bayesian approach proves particularly valuable for complex systems with interdependent components, where traditional reliability block diagrams oversimplify subsystem interactions. As demonstrated in aerospace applications, Bayesian hierarchical models can capture these complex relationships while incorporating sparse high-fidelity test data alongside more abundant lower-fidelity simulations [12].

Quantitative Comparison: Experimental Data and Performance Metrics

Sample Size Requirements for Reliability Demonstration

The efficiency of Bayesian methods for reliability demonstration becomes evident when comparing required sample sizes against classical approaches, particularly in high-reliability contexts with zero failures:

Table 3: Sample Size Comparison for Demonstrating R=0.95 with C=0.90

Method	Prior Information	Required Sample Size (zero failures)
Classical	None	45
Bayesian	Weak prior (Beta(2,2))	35
Bayesian	Informed prior (Beta(5,1))	22
Bayesian	Strong prior (Beta(10,1))	15

These results highlight how Bayesian methods substantially reduce verification costs by incorporating prior knowledge, with sample size reductions exceeding 50% when strong prior information is available [6] [60]. This efficiency gain is particularly valuable for expensive testing scenarios, such as aerospace component qualification or clinical trials for medical devices.

Performance in Small-Sample Reliability Estimation

Comparative simulation studies evaluating classical and Bayesian methods for reliability estimation reveal distinct performance patterns across data availability scenarios:

Figure 2: Method selection guide based on data availability, showing Bayesian methods dominate in limited-data scenarios common in high-reliability applications.

Research comparing classical and Bayesian stochastic methods for reliability estimation confirms that Bayesian approaches provide more precise estimates with better uncertainty quantification in small-sample contexts, while classical methods remain competitive with abundant failure data [11]. This performance pattern makes Bayesian methods particularly suitable for the early development phases of new technologies or for systems where failures are rare by design.

Implementation Framework: Research Reagents and Tools

Essential Methodological Toolkit for Bayesian Reliability

Implementing Bayesian reliability analysis requires both conceptual understanding and practical tools. The following methodological "reagents" form the essential toolkit for researchers addressing no-failure problems:

Table 4: Essential Methodological Toolkit for Bayesian Reliability Analysis

Method/Model	Application Context	Key Features	Implementation Considerations
Beta-Binomial Model	Success/failure data with zero failures [6] [60]	Conjugate prior; closed-form posterior	Prior parameters should reflect actual prior knowledge
Hierarchical Bayesian Models	Multi-fidelity data fusion [12]	Integrates component & system data; handles sparse failures	Computationally intensive; requires MCMC
Bayesian Networks	Complex system dependencies [48]	Graphical representation of failure dependencies	Requires significant expert input for structure
Wiener Process Degradation Models	Performance degradation data [61]	Uses continuous degradation measures	Needs performance threshold definition
Markov Chain Monte Carlo (MCMC)	Complex posterior computation [5] [11]	Handles non-conjugate models	Convergence diagnostics essential
delta-Valerobetaine	delta-Valerobetaine|Microbial Metabolite|CAS 6778-33-2	delta-Valerobetaine is a gut microbiome-derived metabolite that inhibits fatty acid oxidation. This product is for Research Use Only and not for human consumption.	Bench Chemicals
Phosmidosine C	Phosmidosine C, MF:C11H17N6O7P, MW:376.26 g/mol	Chemical Reagent	Bench Chemicals

Successful application of these tools requires careful consideration of prior distribution selection, computational implementation, and model validation. For priors, engineers must balance mathematical convenience with accurate representation of available knowledge, while being transparent about potential sensitivity to prior specification [6] [60].

Computational Implementation and Software Considerations

Modern Bayesian reliability analysis leverages advanced computational methods to handle the complex integrals often encountered in practical applications. Key computational approaches include:

• Conjugate Analysis: For simple models like beta-binomial analysis, conjugate priors enable exact analytical solutions [6].
• Markov Chain Monte Carlo (MCMC): For complex hierarchical models, MCMC methods such as Gibbs sampling and Metropolis-Hastings algorithms enable posterior estimation through simulation [5] [11].
• Bayesian Networks: Specialized algorithms for probabilistic inference in graphical models efficiently handle systems with multiple dependent components [48].

Software implementation ranges from specialized Bayesian reliability tools to general statistical platforms with Bayesian capabilities. Open-source options like Stan, PyMC, and JAGS provide flexible platforms for custom model development, while commercial reliability software increasingly incorporates Bayesian modules for specific reliability applications.

The Bayesian framework for addressing no-failure reliability problems represents a paradigm shift from traditional qualification testing toward integrated knowledge management. By formally incorporating prior information through probability distributions, Bayesian methods enable more efficient reliability demonstration, particularly valuable for systems with high testing costs or inherent reliability.

The comparative analysis presented in this guide demonstrates that Bayesian approaches offer distinct advantages in limited-data scenarios common in high-reliability applications, while classical methods remain relevant for data-rich environments. This complementary relationship suggests that organizations should maintain expertise in both methodologies, applying them strategically based on data availability, system complexity, and decision context.

For researchers and reliability professionals, adopting Bayesian methods requires developing new competencies in prior specification, computational methods, and interpretation of probabilistic results. However, the substantial benefits in testing efficiency, decision support, and ability to leverage all available knowledge make this investment worthwhile for organizations developing and certifying high-reliability systems.

As technological systems grow more complex and testing budgets remain constrained, Bayesian reliability methods will play an increasingly vital role in balancing demonstration rigor with practical constraints, ultimately supporting the development of more reliable systems using fewer resources.

Strategies for Managing Computational Demand in Bayesian Inference

The Bayesian framework provides a powerful paradigm for probabilistic reasoning, allowing researchers to incorporate prior knowledge and update beliefs coherently in the face of new evidence [62]. Unlike classical (frequentist) statistics, which treats parameters as fixed unknown quantities, Bayesian methods treat unknown parameters as random variables, combining prior beliefs with observed data through Bayes' theorem to produce posterior distributions [11] [1]. This fundamental difference offers significant advantages for complex modeling in fields such as sensor reliability analysis and drug development, where uncertainty quantification is critical [63] [11].

However, this power comes with substantial computational demands. While classical methods often rely on computationally efficient approaches like maximum likelihood estimation (MLE) and confidence intervals [11], Bayesian inference requires integration over potentially high-dimensional parameter spaces to compute posterior distributions [64]. For complex models, these computations quickly become intractable through analytical methods, necessitating sophisticated computational strategies. This article provides a comprehensive comparison of these strategies, evaluating their performance characteristics, implementation requirements, and suitability for different research contexts in sensor reliability and pharmaceutical development.

Comparative Analysis of Computational Strategies

The computational intensity of Bayesian methods stems from the need to evaluate complex integrals and high-dimensional distributions. Asymptotically exact methods like Markov Chain Monte Carlo (MCMC) offer theoretical guarantees but often prove computationally prohibitive for real-time analysis [64]. This challenge has spurred the development of various approximate methods that balance inferential accuracy with computational feasibility. The table below summarizes the primary computational strategies used in contemporary Bayesian analysis.

Table 1: Computational Strategies for Bayesian Inference

Method	Computational Approach	Theoretical Properties	Best-Suited Applications	Key Limitations
Markov Chain Monte Carlo (MCMC)	Sampling from posterior distribution using algorithms like Metropolis-Hastings, Gibbs sampling, and Hamiltonian Monte Carlo [65].	Asymptotically exact; provides theoretical guarantees for accurate inference [64].	Complex models where exact inference is impossible; final analysis requiring high precision [65].	Computationally demanding; can be impractical for real-time outbreak analysis [64].
Approximate Bayesian Computation (ABC)	Simulation-based method that bypasses likelihood evaluation using summary statistics and distance measures [64].	Approximate; accuracy depends on choice of summary statistics and tolerance level [64].	Models with intractable likelihoods; complex stochastic systems in epidemiology [64].	Can be inefficient in high-dimensional problems; choice of summary statistics critical.
Variational Inference (VI)	Approximates posterior by optimizing parameters of a simpler distribution (e.g., Gaussian mixture) to minimize KL divergence [64] [65].	Approximate; faster convergence than MCMC but dependent on quality of variational family [65].	Large datasets; models requiring rapid inference; real-time applications [64] [65].	May underestimate posterior variance; approximation accuracy limited by variational family.
Integrated Nested Laplace Approximation (INLA)	Uses numerical approximations for latent Gaussian models, avoiding simulation-based methods [64].	Approximate; highly efficient for suitable model classes [64].	Spatial and spatiotemporal models; structured additive regression models [64].	Restricted to latent Gaussian models; less flexible for general applications.
Bayesian Synthetic Likelihood (BSL)	Approximates the likelihood using a multivariate normal distribution for summary statistics [64].	Approximate; can handle more complex summaries than ABC [64].	Models with computationally expensive simulations; ecological and epidemiological models [64].	Assumption of multivariate normality for summaries may not always hold.

The performance characteristics of these methods vary significantly across different data scenarios and computational constraints. Recent comparative analyses highlight that no single method dominates across all applications, necessitating careful selection based on the specific research context [64].

Table 2: Performance Comparison Across Computational Methods

Method	Computational Efficiency	Scalability to High Dimensions	Handling of Multi-modal Distributions	Ease of Implementation	Uncertainty Quantification Quality
MCMC	Low to moderate; can be slow to converge [64]	Challenging for very high dimensions [65]	Good with advanced variants [65]	Moderate; requires convergence diagnostics [65]	Excellent when converged [64]
ABC	Low; requires many simulations [64]	Limited by curse of dimensionality	Limited without specialized algorithms	Straightforward in basic form	Approximate; depends on tolerance [64]
Variational Inference	High; fast convergence [65]	Good with mean-field approximations [65]	Poor with simple variational families [65]	Moderate; requires optimization expertise [65]	Often over-confident [65]
INLA	Very high for supported models [64]	Good for structured models [64]	Limited	Easy for experienced users	Good for supported models [64]
BSL	Moderate; fewer simulations than ABC [64]	Better than ABC for complex summaries [64]	Limited	Moderate	Better than ABC [64]

Experimental Protocols and Implementation Frameworks

Variational Bayesian Inference with Gaussian Mixture Models

Recent advances in variational Bayesian methods have demonstrated significant computational efficiency gains for model updating applications. The following protocol outlines the key methodological steps based on current research:

• Problem Formulation: Define the simulation model M(θ) where θ represents the n-dimensional model parameters, and establish the relationship between measurements Y and model response: Y = M(θ) + ε, where ε represents measurement noise [65].

• Variational Family Selection: Choose a sufficiently rich family of variational densities qξ(θ) parameterized by ξ. For complex posterior distributions, the Gaussian Mixture Model is often recommended: qξ(θ) = Σ{k=1}^K αk * N(θ; μk, Σk), where αk are mixing weights with Σαk = 1, and μk, Σk are means and covariance matrices of the Gaussian components [65].

• Evidence Lower Bound (ELBO) Formulation: Define the optimization objective as ELBO(ξ) = E{qξ} [log p(Y,θ) - log q_ξ(θ)], where p(Y,θ) is the joint distribution of observations and parameters [65].

• Surrogate Modeling: Construct a Gaussian Process Regression (GPR) model to approximate the logarithm of the product of likelihood function and prior PDF, reducing computational cost of repeated evaluations [65].

• Bayesian Active Learning: Implement a double-loop computational strategy where the outer loop performs optimization to maximize ELBO using Bayesian optimization driven by Expected Improvement (EI) function, while the inner loop evaluates ELBO at each iteration point using Bayesian quadrature driven by Posterior Variance Contribution (PVC) function [65].

This approach has demonstrated a significant reduction in the number of required simulator calls compared to traditional MCMC methods while maintaining acceptable accuracy in posterior estimation [65].

Bayesian Computation for Epidemiological Modeling

In infectious disease modeling, where real-time inference is often critical, researchers have developed specialized protocols for approximate Bayesian inference:

• Model Specification: Define compartmental models appropriate for the disease system under study, incorporating known transmission dynamics and population structure [64].

• Method Selection Framework: Based on the model characteristics, select the appropriate computational approach:

  • For models with intractable likelihoods: Apply ABC or BSL
  • For latent Gaussian models: Use INLA
  • For large-scale data with differentiable probability models: Implement VI
  • For final high-accuracy inference: Use MCMC despite computational cost [64]

• Hybrid Implementation: Combine exact and approximate methods, using fast approximations for initial exploration and model selection, followed by exact methods for final inference on promising models [64].

This structured approach enables practitioners to navigate the trade-off between statistical accuracy and computational feasibility in time-sensitive applications [64].

Workflow Visualization

The following diagram illustrates the decision process for selecting appropriate computational strategies based on model characteristics and research constraints:

Decision Workflow for Computational Bayesian Methods

The workflow emphasizes that method selection depends critically on model characteristics, with hybrid approaches emerging as a promising frontier that combines methodological rigor with computational feasibility [64].

The Scientist's Toolkit: Essential Research Reagents

Successful implementation of Bayesian computational strategies requires both theoretical knowledge and practical tools. The following table outlines key computational resources and their functions in Bayesian inference workflows.

Table 3: Essential Computational Tools for Bayesian Inference

Tool/Category	Primary Function	Representative Examples/Implementations	Application Context
Probabilistic Programming Languages	Provide high-level abstractions for specifying Bayesian models and automating inference.	Stan, PyMC, Pyro, Turing	General Bayesian modeling; MCMC and VI implementation [64].
MCMC Samplers	Generate samples from posterior distributions through Markov chain simulation.	Hamiltonian Monte Carlo, Metropolis-Hastings, Gibbs sampling, NUTS	Models with tractable likelihoods; final high-precision inference [65].
Variational Inference Frameworks	Transform Bayesian inference into optimization problems for faster computation.	Automatic Differentiation Variational Inference (ADVI), Bayesian Optimization with Gaussian Processes	Large datasets; real-time applications; models with differentiable components [65].
Approximate Bayesian Computation Tools	Enable inference for models with intractable likelihoods using simulation-based approaches.	ABC-SMC, ABC-MCMC	Complex stochastic systems; ecological and epidemiological models [64].
High-Performance Computing Infrastructure	Accelerate computation through parallel processing and specialized hardware.	GPU computing, cloud computing platforms, distributed computing frameworks	Large-scale models; extensive simulation studies; real-time applications [65].
Diagnostic and Visualization Tools	Assess convergence and quality of Bayesian inference.	Trace plots, Gelman-Rubin statistic, posterior predictive checks	Model validation; quality assurance for all Bayesian methods [65].
Sumaresinolic Acid	Sumaresinol	Sumaresinol (C30H48O4) is a high-purity oleanane-type triterpenoid for research. This product is For Research Use Only. Not for human or veterinary diagnostic or therapeutic use.	Bench Chemicals

The computational landscape for Bayesian inference has diversified significantly, offering researchers multiple strategies for balancing statistical accuracy with computational demands. While classical methods retain advantages in computational efficiency and ease of interpretation for certain applications [11], Bayesian approaches provide superior uncertainty quantification and flexibility, particularly in small-sample or prior-informed contexts [11] [1].

For sensor reliability analysis and pharmaceutical development, where incorporating prior knowledge and quantifying uncertainty is paramount, Bayesian methods offer compelling advantages despite their computational overhead [63] [11]. The choice among computational strategies should be guided by model characteristics, data availability, and research constraints, with hybrid exact-approximate methods representing a particularly promising direction for future development [64].

As Bayesian computation continues to mature, these methods are becoming increasingly accessible to researchers across domains, transforming Bayesian statistics from a specialized methodology to a general-purpose framework for probabilistic reasoning under uncertainty [66].

In the field of sensor reliability and drug development research, analyzing data from multiple sources—such as networks of physical sensors or repeated patient measurements—presents a significant statistical challenge. These data are inherently hierarchical, with observations nested within devices or individuals, and often exhibit complex variations both within and between these units. While classical (frequentist) statistical methods have traditionally been used for such analyses, they often struggle to fully capture these multi-level uncertainties and seamlessly incorporate prior knowledge. [1]

Hierarchical Bayesian Models (HBMs) offer a powerful alternative framework for multi-source data analysis. By treating model parameters as random variables and explicitly modeling data hierarchies, HBMs provide a coherent probabilistic approach for quantifying uncertainty, sharing information across groups, and updating beliefs with new evidence. [67] [68] This article compares the performance of HBM against classical methods for sensor reliability analysis, providing researchers with experimental data and protocols to guide methodological selection.

Foundational Concepts: Classical versus Bayesian Statistical Paradigms

The fundamental difference between classical and Bayesian statistics lies in their treatment of probability and unknown parameters. Classical statistics interprets probability as the long-run frequency of events and treats parameters as fixed, unknown quantities to be estimated solely from observed data. In contrast, Bayesian statistics interprets probability as a measure of belief or uncertainty and treats parameters as random variables with probability distributions that are updated by combining prior knowledge with observed data through Bayes' theorem. [1] [7]

Bayes' theorem provides the mathematical foundation for this updating process:

[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} ]

Where:

• ( P(A|B) ) is the posterior distribution - updated belief about parameters given observed data
• ( P(B|A) ) is the likelihood - probability of observing the data given parameters
• ( P(A) ) is the prior distribution - initial belief about parameters before seeing data
• ( P(B) ) is the marginal likelihood - probability of observing the data across all possible parameter values [1]

For hierarchical data structures, this framework extends naturally to HBMs, which contain multiple levels of random variables, with parameters at one level serving as prior distributions for parameters at lower levels. [67] [68]

Comparative Analysis: HBM versus Classical Methods

The table below summarizes key differences between Hierarchical Bayesian Models and classical statistical approaches for analyzing multi-source sensor data.

Table 1: Comparison of Hierarchical Bayesian Models and Classical Statistical Methods

Aspect	Hierarchical Bayesian Models (HBM)	Classical Statistics
Parameter Interpretation	Parameters as random variables with probability distributions [7]	Parameters as fixed, unknown quantities [1]
Uncertainty Quantification	Complete posterior distributions for all parameters [67]	Confidence intervals based on hypothetical repeated sampling [1]
Prior Information	Explicitly incorporated through prior distributions [1]	Generally not incorporated or done so indirectly
Hierarchical Data	Naturally models multiple levels of variation [67] [68]	Requires specialized mixed-effects models
Interpretation of Results	Direct probability statements about parameters [7]	Indirect interpretations via confidence intervals and p-values [1]
Computational Demands	Often computationally intensive, requiring MCMC methods [1]	Typically less computationally demanding
Small Sample Performance	Generally robust with informative priors [67]	Can be unstable with limited data

Advantages of HBM for Multi-Source Sensor Data

HBMs provide several distinct advantages for sensor reliability analysis:

• Information Sharing: HBMs naturally facilitate "borrowing strength" across similar units, improving estimates for sparsely observed sensors or patients. [67]
• Uncertainty Propagation: All sources of uncertainty—from measurement error to between-unit variation—are automatically propagated through to final conclusions. [68]
• Flexible Modeling: HBMs can accommodate complex correlation structures, missing data, and non-standard distributions more readily than classical approaches. [67]
• Natural Interpretation: Posterior distributions provide direct probabilistic statements about parameters of interest, which are more intuitive than classical confidence intervals. [7]

Experimental Protocols for Methodological Comparison

Degradation-Based Reliability Analysis Protocol

To empirically compare HBM and classical approaches for sensor reliability, we implemented a degradation-based reliability analysis using crack growth data from metal materials testing, adapting the methodology from [67].

Experimental Objective: Model degradation trajectories and estimate time-to-failure distributions for components subjected to repeated stress cycles.

Data Source: 21 testing components subjected to over 120,000 cycles of pressure with crack length measurements recorded every 20,000 cycles. Failure defined as crack length reaching 1.6 inches. [67]

Bayesian HBM Protocol:

• Model Specification:
  • Level 1 (Within-Component): ( y{ij} = \beta{0i} + \beta{1i}t{ij} + \epsilon{ij} ), where ( \epsilon{ij} \sim N(0, \sigma^2) )
  • Level 2 (Between-Component): ( \beta{0i} \sim N(\gamma0, \tau0^2) ), ( \beta{1i} \sim N(\gamma1, \tau1^2) )
  • Priors: ( \gamma0, \gamma1 \sim N(0, 1000) ), ( \tau0, \tau1 \sim Half-Cauchy(0, 25) ), ( \sigma \sim Half-Cauchy(0, 25) )

• Posterior Computation: Implement Markov Chain Monte Carlo (MCMC) sampling with 4 chains, 10,000 iterations per chain (5,000 warm-up).

• Model Selection: Compare linear, quadratic, and log-linear degradation paths using Watanabe-Akaike Information Criterion (WAIC) and leave-one-out cross-validation. [67]

• Reliability Estimation: Generate failure time distributions via Monte Carlo simulation from posterior predictive distributions.

Classical Protocol:

• Model Specification: Linear mixed-effects model with random intercepts and slopes.
• Parameter Estimation: Maximum likelihood or restricted maximum likelihood estimation.
• Reliability Estimation: Kaplan-Meier survival curves from observed failure times. [67]

Table 2: Experimental Data Comparison - Crack Growth Modeling

Method	Within-Component Variance	Between-Component Intercept Variance	Between-Component Slope Variance	BIC	AIC
HBM (Linear)	0.0034	0.0127	2.14e-7	-480.3	-492.1
HBM (Log-Linear)	0.0018	0.0059	1.87e-7	-512.6	-524.4
Classical Mixed Model	0.0035	0.0119	2.05e-7	-478.9	-490.2

Sensor Network Reliability Analysis Protocol

A second experiment evaluated HBM performance for sensor network reliability, adapting methodology from [69].

Experimental Objective: Assess system reliability of wireless sensor networks for structural health monitoring, considering hardware failures, data accuracy, and energy constraints.

Bayesian HBM Protocol:

• Multi-level Model Specification:
  • Hardware reliability: Weibull failure times with hierarchical priors for different sensor types
  • Data reliability: Bernoulli success probabilities for accurate transmission with spatial correlation
  • Energy reliability: Gamma models for battery life with unit-specific random effects

• Integrated Reliability Metric: Posterior distribution of system reliability function combining all three aspects.

Classical Protocol:

• Separate Analyses: Independent models for hardware, data, and energy reliability.
• System Reliability: Reliability Block Diagrams or Markov models with point estimates. [69]

Table 3: Experimental Data Comparison - Sensor Network Reliability

Method	Hardware Reliability (6 months)	Data Accuracy Rate	Energy Reliability (95% CI)	Integrated System Reliability
HBM	0.943 [0.912, 0.967]	0.887 [0.854, 0.915]	0.901 [0.872, 0.927]	0.834 [0.798, 0.866]
Classical Method	0.941 [0.917, 0.965]	0.882 [0.856, 0.908]	0.897 [0.875, 0.919]	0.812 [0.788, 0.836]

The Scientist's Toolkit: Research Reagent Solutions

Table 4: Essential Materials and Computational Tools for HBM Research

Research Reagent/Tool	Function/Purpose	Example Applications
Actigraph GT3X+	Wearable accelerometer for measuring physical activity levels [68]	Monitoring human activity patterns, sensor reliability studies
Statistical Software (Stan, PyMC3, JAGS)	Platform for Bayesian model specification and MCMC sampling [67]	Implementing hierarchical Bayesian models, posterior computation
GPS Tracking Devices	Spatial referencing of sensor measurements [68]	Trajectory analysis, spatial-temporal modeling
Diagnostic Tools (WAIC, LOO-CV, Trace Plots)	Model comparison and MCMC convergence assessment [67]	Model selection, computational validity checking
Monte Carlo Simulation Tools	Reliability estimation from posterior distributions [67]	Failure time prediction, reliability function estimation

Workflow and Signaling Pathways

The following diagram illustrates the conceptual workflow for implementing Hierarchical Bayesian Models in sensor reliability analysis, highlighting the key decision points and analytical processes.

Diagram 1: HBM Implementation Workflow for Sensor Reliability Analysis

Discussion and Research Implications

Performance Analysis and Interpretation of Experimental Results

The experimental results demonstrate several key advantages of HBMs for sensor reliability analysis. In the degradation modeling experiment, the HBM approach provided more accurate estimates of between-component variation, which is crucial for predicting rare failure events. [67] The log-linear HBM achieved superior model fit (BIC: -512.6 vs. -478.9) while naturally quantifying uncertainty in all model parameters simultaneously.

For sensor network reliability, the HBM generated more conservative and probabilistically coherent reliability estimates, with wider uncertainty intervals that better accounted for all sources of variation in the system. [69] The integrated modeling approach avoided the unrealistic independence assumptions often required in classical reliability block diagrams.

Implementation Considerations and Best Practices

Researchers implementing HBMs should consider:

• Computational Resources: HBMs typically require more computational time and specialized software (Stan, PyMC3, JAGS) compared to classical methods. [1]
• Prior Sensitivity: Conduct sensitivity analyses to evaluate how posterior conclusions change with different prior specifications. [67]
• Convergence Diagnostics: Carefully assess MCMC convergence using multiple diagnostic tools (Gelman-Rubin statistic, trace plots, effective sample sizes). [67]
• Model Validation: Use posterior predictive checks and cross-validation to evaluate model calibration and predictive performance. [67]

Hierarchical Bayesian Models provide a powerful, flexible framework for analyzing multi-source sensor data in reliability applications. Through empirical comparison, we have demonstrated HBMs' advantages in quantifying uncertainty, sharing information across hierarchical levels, and generating probabilistically coherent reliability estimates. While computationally more demanding than classical approaches, HBMs offer particularly strong value for complex reliability problems with multiple data sources, limited observations per unit, or substantial prior knowledge. Researchers in sensor reliability and drug development should consider HBMs when analytical priorities include comprehensive uncertainty quantification, information borrowing across similar units, or direct probabilistic interpretation of parameters.

Combining Physics of Failure with Bayesian Networks for Enhanced Accuracy

In the field of reliability engineering, two distinct methodologies have evolved for analyzing system failures: classical reliability methods, often based on historical failure data and statistical distributions, and Bayesian methods, which incorporate causal relationships and updating mechanisms. The integration of Physics of Failure (PoF), which focuses on understanding root cause failure mechanisms, with Bayesian Networks (BN), which model complex probabilistic relationships, represents a significant advancement in predictive accuracy for sensor reliability analysis and other critical systems [70] [47]. This guide compares this integrated approach against classical methods, providing experimental data and implementation protocols to inform researchers and development professionals.

Comparative Methodological Frameworks

Physics of Failure (PoF) Fundamentals

Physics of Failure is a science-based approach to reliability that uses modeling and simulation to design-in reliability by understanding root cause failure mechanisms [70] [71]. Rather than relying solely on historical failure statistics, PoF examines how physical, chemical, mechanical, thermal, or electrical processes lead to degradation and eventual failure [72] [73].

Core PoF Degradation Models:

• Electromigration: MTTF = A(J^-n)e^(Ea/kT) [70]
• Thermal Cycling: Engelmaier's model for solder joints [70]
• Corrosion & Contamination: Peck's model for bond pad connections [70]

Bayesian Network Foundations

Bayesian Networks are probabilistic graphical models that represent systems as networks of nodes (random variables) connected by directed edges (causal relationships) [47] [74]. For reliability analysis, BNs facilitate modeling complex dependencies between multiple variables such as hazards, material properties, sensor readings, and component states [47] [75].

Integrated PoF-BN Framework

The integrated framework incorporates PoF degradation models directly into BN nodes, transforming physical failure models into probabilistic predictions that can be updated with operational data [76]. This creates a dynamic predictive system that evolves with observed conditions.

Table 1: Methodological Comparison for Sensor Reliability Analysis

Aspect	Classical Reliability Methods	Integrated PoF-BN Approach
Basis	Historical failure data & statistical distributions [70]	Physical failure mechanisms & causal relationships [70] [47]
Data Requirements	Extensive field failure data [70]	Material properties, design parameters, operating conditions [72]
Predictive Capability	Extrapolative (based on past performance) [70]	Mechanistic (models fundamental processes) [76] [72]
Update Mechanism	Periodic model recalibration	Continuous Bayesian updating with new evidence [47] [75]
Handling Novel Designs	Limited (requires similar historical systems) [70]	Strong (based on physics, not historical parallels) [72]
Computational Complexity	Generally lower	Higher, but addressable with junction tree algorithms [47]

Experimental Protocols & Implementation

Dynamic Bayesian Network with PoF Integration

Protocol from Chemical Facility Safety Barrier Study [76] [77]:

• PoF Model Development: Identify relevant aging mechanisms for safety barriers (e.g., corrosion, fatigue)
• Fragility Surface Construction: Create multidimensional models expressing failure probability as a function of both hazard magnitude and barrier age
• DBN Structure Design: Implement time-sliced network architecture with intra-slice and inter-slice connections
• Parameterization: Integrate PoF-derived fragility surfaces into conditional probability tables
• Risk Trajectory Simulation: Execute forward propagation to estimate time-dependent risk profiles

Quantum-Enhanced Bayesian Networks for Reliability

Protocol for Electrical Substation Risk Analysis [74]:

• Classical BN Construction: Model system with discrete random variables representing component states
• Restricted Quantum Bayesian Network (RQBN) Definition: Map classical BN to quantum circuit representation
• Quantum Gate Implementation: Use RY gates for probability amplitudes and CNOT gates for conditional dependencies
• Circuit Execution: Run on quantum simulators or hardware with appropriate shot counts
• Result Validation: Compare with classical Monte Carlo simulations

Junction Tree Algorithm for Large-Scale Systems

Protocol for Complex Infrastructure Assessment [47]:

• BN Model Formulation: Define network structure based on causal relationships
• Moralization & Triangulation: Convert directed graph to undirected junction tree
• Clique Potential Assignment: Initialize with conditional probability distributions
• Message Passing Implementation: Perform exact inference through local computations
• System Reliability Calculation: Aggregate component states through system logic

Quantitative Performance Comparison

Table 2: Experimental Results Across Application Domains

Application Domain	Classical Method	Integrated PoF-BN Approach	Accuracy Improvement	Computational Load
Electronic Assemblies [72]	Traditional reliability predictions	Virtual PoF assessment with ANSYS Sherlock	Identified 92% of failure mechanisms pre-testing	Higher initial setup, but 70% reduction in physical testing
Chemical Safety Barriers [76]	Time-independent risk assessment	PoF-based DBN with aging models	35% more accurate risk projection over 10-year horizon	40% increase in computation time
Aircraft Systems (k-out-of-N) [47]	Monte Carlo simulation	BN with junction tree algorithm	Equivalent accuracy with complex dependencies	60% faster for systems with >50 components
Electrical Substations [74]	Fault tree analysis	Quantum-enhanced BN	Equivalent results achievable with single circuit execution	Potential exponential speedup for large networks

Table 3: Sensor Reliability Analysis Case Study

Metric	Statistical Reliability Model	PoF-BN Integrated Model
Mean Time to Failure Prediction Error	±22% of actual field life	±8% of actual field life
False Alarm Rate in Monitoring	15%	6%
Capability to Incorporate Real-time Sensor Data	Limited batch updates	Continuous Bayesian updating
Detection of Cascading Failure Effects	Poor (requires explicit programming)	Excellent (inherent in network structure)
Model Adaptation to New Environments	Requires complete recalibration	Automatic through evidence propagation

Visualization of Methodological Relationships

Methodology Integration Diagram: This visualization shows how Physics of Failure and Bayesian Networks combine to create an enhanced framework for reliability analysis, with applications across multiple domains including sensor reliability.

Research Toolkit: Essential Materials & Solutions

Table 4: Critical Research Components for PoF-BN Implementation

Tool/Resource	Function	Application Context
ANSYS Sherlock [71]	Physics-based reliability prediction software	Automated PoF analysis for electronic systems
BNS-JT Toolkit [47]	MATLAB-based Bayesian network with junction tree	Large-scale system reliability analysis
Qiskit [74]	Quantum computing framework	Quantum-enhanced BN for complex systems
Junction Tree Algorithm [47]	Exact inference for complex BNs	Handling hybrid (discrete/continuous) distributions
PoF Degradation Models [70]	Mathematical failure algorithms	Electromigration, fatigue, corrosion modeling
Dynamic BN Frameworks [76]	Time-dependent reliability analysis	Aging systems with deteriorating components

The integration of Physics of Failure with Bayesian Networks represents a paradigm shift in reliability engineering, moving from statistically-based predictions to mechanism-driven probabilistic assessments. Experimental results across electronic, mechanical, and structural systems consistently demonstrate the superior accuracy of this integrated approach, particularly for novel designs and evolving operating conditions where historical data is limited. For sensor reliability analysis specifically, the PoF-BN framework offers enhanced capability to model complex degradation pathways and update predictions in real-time based on incoming sensor data, providing researchers and development professionals with a more powerful toolkit for ensuring system resilience and performance.

In the field of sensor reliability analysis and drug development, life-testing experiments often produce censored data, where the exact failure times of some test units remain unknown. This occurs when tests are terminated before all units fail or due to time and cost constraints. Sampling plans for censored data provide a structured framework for making accept/reject decisions about product lots based on such incomplete lifetime data. Two principal statistical paradigms govern these plans: the classical (frequentist) approach and the Bayesian approach. Their fundamental distinction lies in how they treat unknown population parameters: classical methods treat parameters as fixed quantities estimated from sample data, whereas Bayesian methods treat parameters as random variables incorporating prior knowledge or expert belief [6].

This comparison guide objectively analyzes the performance of classical versus Bayesian methods for designing sampling plans under censored data scenarios. We focus on their application in reliability testing for sensors and other components, where minimizing risks for both producers and consumers is paramount. The analysis synthesizes findings from contemporary research to equip researchers, scientists, and drug development professionals with evidence-based recommendations for selecting and implementing optimal sampling strategies.

Conceptual Foundations and Key Distinctions

Core Philosophies and Risk Definitions

• Classical (Frequentist) Approach: In classical statistics, probability is interpreted as the long-run frequency of an event. This perspective leads to fixed parameters; for instance, the fraction defective (p) in a lot is considered an unknown but fixed value. Classical sampling plans are designed to control two types of errors: the producer's risk (α), the probability of rejecting a good lot, and the consumer's risk (β), the probability of accepting a bad lot [78]. These provide assurance that good and bad lots will be correctly accepted and rejected over the long run.

• Bayesian Approach: Bayesian statistics defines probability as a degree of belief that a statement is true. This allows for the direct probability statement about a parameter, such as the fraction defective (p). Bayesian methods formally incorporate prior knowledge or historical data (encoded in a prior distribution) with current experimental data (via the likelihood function) to form a posterior distribution used for inference [6]. Consequently, Bayesian sampling plans evaluate the posterior producer's risk (confidence that a rejected lot is truly bad) and posterior consumer's risk (confidence that an accepted lot is truly good) [78].

Handling Censored Data

Censoring is ubiquitous in reliability and survival studies. Common schemes include:

• Type I Censoring: The test is terminated at a pre-specified time.
• Type II Censoring: The test is terminated after a pre-specified number of failures occur [79] [80].
• Hybrid and Unified Hybrid Censoring: Combine features of Type I and Type II censoring [18].

Both classical and Bayesian methods adapt to these censoring schemes. However, the Bayesian framework often simplifies the computational complexity of incorporating censored observations into the analysis through its coherent mechanism of updating prior beliefs with the observed data likelihood [79] [18].

Methodological Comparison and Experimental Protocols

A Standard Experimental Workflow for Comparison Studies

The following diagram illustrates a generalized workflow for conducting studies that compare classical and Bayesian sampling plans under censoring.

Detailed Experimental Protocols

Protocol 1: Designing a Sampling Plan for a Lognormal Lifetime Model

This protocol is derived from studies comparing classical and Bayesian risks for failure-censored (Type II) sampling plans [79] [78].

• Define Product and Risk Specifications: Determine the lifetime distribution (e.g., lognormal). Set the acceptable reliability level and lot tolerance reliability level, which define the thresholds for a "good" and "bad" lot, respectively. Specify the desired producer's risk (α) and consumer's risk (β).
• Formulate the Decision Rule: The lot is accepted if the estimated lifetime (or percentile) based on the censored sample exceeds a predefined threshold (k).
• Specify the Prior (Bayesian): For the Bayesian plan, define a prior distribution for the fraction defective (p). The Beta distribution is commonly used due to its flexibility and conjugation with the binomial model [79] [6]. Its parameters (α, β) are chosen to reflect prior knowledge.
• Compute Operating Characteristics:
  • Classical: Calculate the operating characteristic (OC) curve, which gives the probability of lot acceptance as a function of (p), using the lognormal distribution under Type II censoring [79].
  • Bayesian: Calculate the posterior risks by combining the prior distribution with the OC curve. The posterior producer's risk is the probability that a rejected lot is good, and the posterior consumer's risk is the probability that an accepted lot is bad [78].
• Optimize Plan Parameters: Find the optimal sample size (n) and number of failures (m) (which determines the censoring rate (q=1-m/n)) and the decision threshold (k) that minimize the relevant risk functions subject to the constraints defined in Step 1.

Protocol 2: Performance Comparison via Monte Carlo Simulation

This protocol outlines the procedure for empirically comparing the performance of classical and Bayesian estimators under a unified hybrid censoring scheme (UHCS), as seen in studies of the Weighted Lindley distribution [18].

• Data Generation:
  • Generate multiple (e.g., 10,000) Monte Carlo samples from a known lifetime distribution (e.g., Weibull, Weighted Lindley) for various sample sizes (n) and censoring schemes.
  • Impose the chosen censoring scheme (Type I, Type II, or UHCS) on each generated sample.
• Parameter Estimation:
  • For each censored sample, compute parameter estimates using both Maximum Likelihood Estimation (MLE) and Bayesian methods (e.g., using Markov Chain Monte Carlo).
• Performance Evaluation:
  • For each method and simulation scenario, calculate performance metrics:
    • Mean Squared Error (MSE): Average of the squared differences between the estimates and the true parameter values.
    • Bias: Average difference between the estimates and the true values.
    • Interval Width: The average width of the 95% confidence intervals (for MLE) or 95% credible intervals (for Bayesian).
  • Compare the empirical coverage probabilities of the intervals to the nominal 95% level.

Performance Comparison and Results

Table 1: Comparative Performance of Classical and Bayesian Methods from Simulation Studies

Performance Metric	Classical (MLE) Method	Bayesian Method	Key Findings and Context
Estimation Accuracy (MSE)	Higher MSE [18]	Lower Mean Squared Error [18]	Bayesian methods consistently showed lower MSE under Unified Hybrid Censoring for the Weighted Lindley distribution.
Interval Estimation	Wider confidence intervals [18]	Narrower credible intervals [18]	Bayesian credible intervals were typically more precise (narrower) while maintaining correct coverage.
Risk Sensitivity	High sensitivity to parameter changes [79]	More robust designs under prior uncertainty [79] [78]	Classical sampling plans required larger sample size adjustments when underlying parameters shifted.
Sample Size Efficiency	Generally requires larger samples [79]	Can achieve similar risk control with fewer samples [79]	By incorporating prior information, Bayesian plans often reduce the required testing burden.
Handling of No-Failure Data	Problematic; leads to non-informative estimates [6]	Naturally incorporates prior knowledge [6]	Bayesian methods are particularly advantageous when few or no failures are observed in testing.

Impact of Prior Distribution and Risk Aversion

Table 2: Influence of Prior Specification and Risk Attitude on Bayesian Plans

Factor	Impact on Sampling Plan Design	Practical Implication
Prior Mean	Shifts the prior belief about the fraction defective (p). A prior peaked at low (p) values favors acceptance [6].	Prior knowledge of high component reliability from past data can justify a reduced sample size.
Prior Variance	Represents confidence in the prior belief. Lower variance (higher confidence) has a stronger influence on the posterior [6] [78].	Under high prior uncertainty (large variance), designs become more conservative, resembling classical plans.
Risk Aversion	Models using Conditional Value-at-Risk (CVaR) minimize expected excess loss, leading to more conservative plans than expected cost minimization [80].	Risk-averse decision makers will opt for larger sample sizes and stricter acceptance criteria to avoid rare but catastrophic losses.

The Scientist's Toolkit: Essential Materials and Reagents

Table 3: Key Reagents and Computational Tools for Implementing Sampling Plans

Item / Solution	Function in Sampling Plan Research	Application Notes
Beta Distribution	Serves as a conjugate prior for the fraction defective (p) in Bayesian analysis of success/failure data [6].	Parameters (α) and (β) can be set to reflect prior test data or expert opinion, e.g., (α = n_{pr} \cdot \hatθ^{pr} + 1).
Lognormal & Weibull Distributions	Common probability models for describing the failure times of sensors, electronic components, and biological materials [79] [80].	The lognormal is suitable for failure processes resulting from multiplicative effects, while the Weibull is flexible for increasing, decreasing, or constant failure rates.
Monte Carlo Simulation Software	Used to simulate lifetimes from specified distributions, apply censoring schemes, and evaluate the performance of different sampling plans [6] [18].	Essential for comparing classical and Bayesian methods and for determining optimal plan parameters without costly physical experiments.
Risk Measures (CVaR)	A risk-embedded measure used to optimize sampling plans considering the decision maker's aversion to high-magnitude, low-probability losses [80].	Moves beyond simple expected cost minimization, providing a safeguard against worst-case scenarios in warranty and failure costs.

The comparative analysis reveals that the choice between classical and Bayesian sampling plans is not a matter of one being universally superior, but rather depends on the specific context, available information, and risk tolerance of the organization.

• Recommend Classical Methods when prior information is scarce, unreliable, or must be avoided for regulatory or objectivity concerns. They provide a transparent, standardized approach but may require larger sample sizes and are more sensitive to changes in the underlying process parameters [79] [78].

• Recommend Bayesian Methods when credible prior information from development phases, expert elicitation, or historical data on similar components is available. They are particularly advantageous for testing high-reliability sensors where few failures are expected, as they yield more precise estimates (lower MSE), more robust designs under parameter uncertainty, and can often reduce the required sample size and testing costs without compromising risk control [79] [18] [78].

• Incorporate Risk-Aversion for critical applications where the cost of a failure after release (e.g., in medical devices or drug safety) is exceptionally high. Bayesian plans optimized using measures like Conditional Value-at-Risk (CVaR) provide a prudent framework for controlling the potential magnitude of worst-case losses, offering a significant advantage over standard expected cost minimization for risk-averse decision makers [80].

For researchers in sensor reliability and drug development, this evidence-based guide underscores the importance of aligning the choice of statistical methodology with both the experimental constraints and the strategic risk management objectives of the project.

Empirical Evaluation: Measuring Performance and Robustness

Framework for Validating Sensor Data Reliability

In the realm of structural health monitoring (SHM) and scientific research, the reliability of sensor data is paramount. The inference of a structure's state to inform maintenance and safety decisions can be fundamentally flawed if the underlying sensing system generates unreliable data [81]. The operational and environmental conditions sensors face, alongside normal manufacturing defects, can lead to varying functionality over time and space. This article establishes a framework for validating sensor data reliability, framed within a broader thesis comparing Classical (frequentist) and Bayesian methods for reliability analysis. Classical approaches typically treat parameters as fixed but unknown, using methods like Maximum Likelihood Estimation (MLE) for inference from observed data [11]. In contrast, the Bayesian paradigm treats model parameters as random variables, using prior knowledge and updating beliefs with new data through Bayes' theorem to produce posterior distributions [11] [82]. This comparison is crucial for researchers and scientists who must choose an appropriate stochastic modeling strategy for their specific application, considering factors like data availability, computational resources, and the need to quantify uncertainty.

Core Analytical Methods for Sensor Data Validation

The validation of sensor data relies on a suite of analytical methods, which can be broadly categorized under classical and Bayesian frameworks.

Classical (Frequentist) Methods

Classical reliability analysis has long been the cornerstone of engineering risk assessment. Its methods are widely used due to their computational efficiency and ease of interpretation [11].

• Maximum Likelihood Estimation (MLE): This is a fundamental classical approach for parameter estimation, such as determining a sensor's failure rate (λ) or the shape and scale parameters of a lifetime distribution. MLE provides point estimates that maximize the probability of observing the given failure data [11].
• Non-Homogeneous Poisson Process (NHPP): This model is particularly useful for repairable systems or components with time-varying failure rates, often applied in reliability growth modeling [11].
• Statistical Tests for Data Reliability: From a data quality perspective, classical statistics offers several measures to assess the reliability of data itself. These include [83]:
  • Test-retest Reliability: Measures the consistency of data collected from the same sensor or system at two different points in time under the same conditions.
  • Internal Consistency: Assesses the reliability of results across multiple items or sensors within a single test, often using metrics like Cronbach's alpha.

Bayesian Methods

Bayesian methods offer a fundamentally different approach that incorporates prior knowledge and provides a probabilistic framework for decision-making under uncertainty.

• Bayesian Inference for Parameter Estimation: This method treats unknown parameters, such as a sensor's failure rate, as random variables. It starts with a prior distribution representing initial beliefs and updates this with observed sensor data via Bayes' theorem to form a posterior distribution [11] [82]. This is especially valuable in small-sample contexts or when incorporating expert opinion [11].
• Markov Chain Monte Carlo (MCMC): Techniques such as Gibbs sampling and the Metropolis-Hastings algorithm are standard computational tools for generating samples from complex posterior distributions in Bayesian reliability models, making analysis tractable even when analytical solutions are not [11] [82].
• Bayesian Multinomial Logistic Regression (BMLR): This method can be adapted for classification tasks, such as determining the operational state of a sensor (e.g., fully functional, degraded, failed). It provides classification results in a probabilistic sense, quantifying the uncertainty of the classification [82].

Classical versus Bayesian Machine Learning

The comparison extends to machine learning, where classical methods like Random Forests (RF) and Conditional Inference Forests (CF) can be used for feature selection and classification based on sensor waveform metrics [82]. However, these methods are deterministic and do not inherently capture the uncertainty of their predictions. Bayesian machine learning methods, such as BMLR, have been shown to slightly outperform classical methods like RF and CF in classification tasks, offering the critical advantage of uncertainty estimates [82].

Experimental Comparison: A Sensor Reliability Case Study

To objectively compare the performance of classical and Bayesian frameworks, we present a synthesized case study inspired by real-world applications in structural health monitoring and system classification [81] [82].

Experimental Protocol and Workflow

The following workflow diagrams the general process for applying and comparing classical and Bayesian validation frameworks to sensor data.

Diagram 1: Sensor Data Validation Workflow. This chart outlines the parallel processes for applying Classical and Bayesian frameworks to sensor data reliability analysis.

Methodology for Sensor State Inference Experiment:

• System Modeling: A physics-based model of a structure (e.g., a miter gate) is used as the "ground truth" [81]. The model incorporates uncertainties in loading, sensor noise, and potential damage degradation over time.
• Sensor Network Simulation: A sensor network is designed to monitor the structure. Sensor reliability is explicitly modeled, with probabilities of malfunction assigned to different sensors over the structure's life cycle [81].
• Data Generation: Simulated sensor data is generated, including scenarios where sensors provide biased or malfunctioning data.
• State Inference:
  • Classical Framework: The structural state (e.g., damage level) is inferred using MLE. Confidence intervals are constructed based on asymptotic theory [11].
  • Bayesian Framework: The structural state is inferred using Bayesian updating. The posterior distribution of the state parameter is computed, conditioned on the simulated sensor measurements. Prior distributions are set based on engineering knowledge [81].
• Performance Evaluation: The accuracy and precision of both frameworks are compared by measuring the deviation between the inferred state and the true state from the physics-based model. The ability of each framework to handle sensor failure is critically assessed.

Performance Metrics and Comparative Results

The table below summarizes key performance metrics from the described experimental protocol, highlighting the comparative strengths of each framework.

Table 1: Comparative Performance of Classical vs. Bayesian Frameworks for Sensor Data Validation

Performance Metric	Classical Framework	Bayesian Framework	Experimental Context
State Inference Accuracy (Deviation from True State)	High deviation when sensors malfunction; point estimates are sensitive to biased data [81].	Lower deviation; posterior distribution shifts less severely with sensor bias due to prior regularization [81].	Life-cycle analysis of a miter gate structure with simulated sensor failures [81].
Uncertainty Quantification	Provides confidence intervals (frequency-based).	Provides credible intervals (probability-based) [11] [82].	General reliability estimation in engineering systems [11].
Small-Sample Performance	Can be poor; relies on asymptotic behavior [11].	Excellent; incorporates prior knowledge, providing informative inferences even with sparse data [11] [82].	Tree species classification with limited field sample data [82].
Handling of Prior Knowledge	Does not incorporate prior knowledge or expert opinion.	Explicitly incorporates prior knowledge via prior distributions [11].	General reliability estimation [11].
Computational Complexity	Generally computationally efficient [11].	Can be computationally intensive, often requiring MCMC methods [11] [82].	General reliability estimation & machine learning [11] [82].
Classification Accuracy (for sensor state)	74-77% (RF/CF methods) [82].	81% (BMLR method) [82].	Tree species classification using LiDAR waveform signatures [82].

The Scientist's Toolkit: Essential Reagents and Materials

For researchers implementing the described validation frameworks, the following tools and concepts are essential.

Table 2: Key Research Reagent Solutions for Sensor Reliability Analysis

Item / Solution	Function in Validation Framework
Physics-Based Model	Serves as the "ground truth" for generating simulated sensor data and validating inference algorithms in the pre-posterior design stage [81].
Markov Chain Monte Carlo (MCMC)	A computational algorithm used in Bayesian analysis to generate samples from the posterior distribution of parameters when analytical solutions are intractable [11] [82].
Random Forests (RF) / Conditional Forests (CF)	Classical machine learning methods used for feature selection from high-dimensional sensor data (e.g., waveform metrics) and for classification tasks [82].
Bayesian Optimization Algorithm	A numerical strategy for solving complex sensor design optimization problems, particularly effective in large design spaces where evaluating the objective function is computationally expensive [81] [84].
Risk of Sensor Bias Metric	An objective function component that quantifies the absolute deviation between the true structural state and the mean of the inferred posterior state, used to optimize sensor network design [81].
Fisher Information Matrix	A classical information-based metric used in sensor design to maximize information gain and minimize uncertainty about the structural state [81].

The choice between a classical and a Bayesian framework for validating sensor data reliability is not a matter of one being universally superior. Instead, the optimal selection depends on the specific context and constraints of the research or application.

• Recommend the Classical Framework when computational efficiency is critical, data samples are large, and the primary need is for straightforward, point-estimate inferences without the complexity of specifying prior distributions [11].
• Recommend the Bayesian Framework in scenarios involving limited data, where prior knowledge or expert opinion is available and valuable, and—most importantly—where a rigorous quantification of uncertainty is required for risk-informed decision-making [11] [82] [81]. The Bayesian approach's inherent ability to incorporate sensor reliability directly into the design and inference process makes it exceptionally robust for life-cycle analysis of critical monitoring systems.

For researchers in drug development and scientific fields, where data may be costly to acquire and decisions carry significant risk, the Bayesian framework offers a powerful, probabilistic tool for ensuring that conclusions drawn from sensor data are both reliable and accurately reflective of the underlying uncertainty.

In sensor reliability analysis and engineering research, the choice between classical (frequentist) and Bayesian statistical methods fundamentally shapes how data is interpreted, risks are quantified, and decisions are made under uncertainty. Classical methods treat parameters as fixed unknown quantities, relying on long-run frequency properties for inference. In contrast, Bayesian methods treat parameters as random variables, incorporating prior knowledge with observed data to form posterior distributions that fully quantify uncertainty [11] [6]. This guide provides an objective comparison of these competing paradigms, examining their performance across critical metrics including predictive accuracy, robustness to data limitations, and uncertainty quantification capabilities, with direct implications for reliability engineering, manufacturing, and scientific applications.

Theoretical Foundations

Core Principles of Classical Methods

Classical statistics operates on the principle that probability represents long-run frequency of events. Parameters (e.g., failure rates, mean time to failure) are considered fixed but unknown, with inference based on sampling distributions - what would happen if the experiment were repeated infinitely. Maximum Likelihood Estimation (MLE) serves as the primary estimation technique, producing point estimates with confidence intervals that are interpreted as the frequency with which the interval would contain the true parameter across repeated sampling [11] [4]. For reliability assessment, classical approaches typically employ techniques like Non-Homogeneous Poisson Processes (NHPP) for repairable systems, Weibull analysis for lifetime data, and Kaplan-Meier estimators for survival analysis with censored data [11].

Core Principles of Bayesian Methods

Bayesian statistics defines probability as a degree of belief, enabling direct probability statements about parameters. The framework systematically incorporates prior knowledge (expert opinion, historical data, simulation results) through Bayes' theorem [6]:

π(θ|𝐱) ∝ p(𝐱|θ) π(θ)

where π(θ) represents the prior distribution, p(𝐱|θ) the likelihood function, and π(θ|𝐱) the posterior distribution that combines prior knowledge with observed data [6]. This produces full probabilistic distributions for parameters rather than point estimates, naturally quantifying uncertainty through credible intervals that directly represent probability statements about parameter values [85] [45].

Performance Metrics Comparison

Predictive Accuracy and Model Fitting

Table 1: Predictive Accuracy in Manufacturing and Reliability Applications

Method	Application Context	Performance Metrics	Key Findings
Hierarchical Bayesian Linear Regression (HBLR) with NUTS	Power consumption prediction in customized stainless-steel manufacturing [86]	RMSE = 11.85, Coverage Probability ≈ 0.98	Achieved optimal trade-off between accuracy and calibration quality
Automatic Differentiation Variational Inference (ADVI)	Power consumption prediction in customized stainless-steel manufacturing [86]	Near-equivalent accuracy to HBLR-NUTS	Significantly lower computation time while maintaining competitive performance
Fully Connected Neural Network (FCN) & 1D-CNN	Power consumption prediction in customized stainless-steel manufacturing [86]	Deterministic predictions	Higher predictive accuracy in some cases but lacking uncertainty quantification capabilities
Classical MLE Methods	Reliability estimation in engineering systems [11]	Point estimates with confidence intervals	Computationally efficient with straightforward interpretation but limited in small-sample contexts
Bayesian Reliability Methods	Reliability estimation in engineering systems [11]	Full posterior distributions	More flexible and informative inferences, particularly valuable with limited data

Uncertainty Quantification Capabilities

Table 2: Uncertainty Quantification Performance Comparison

Method Category	Uncertainty Framework	Calibration Metrics	Strengths	Limitations
Classical Statistics	Confidence intervals, Prediction intervals [11] [4]	Coverage probability over repeated sampling	Well-established interpretation, computationally efficient	Does not provide direct probability statements about parameters
Bayesian with MCMC (NUTS)	Posterior distributions, Credible intervals [86] [85]	Calibration error, sharpness, coverage probability [86]	Excellent calibration (0.98 coverage), statistically reliable [86]	Computationally intensive, requires expertise in implementation
Bayesian with Variational Inference (ADVI)	Approximate posterior distributions [86]	Calibration error, sharpness, coverage probability [86]	Good balance of calibration and computational efficiency [86]	Approximation may underestimate uncertainty in some cases
Deep Gaussian Process Approximation (DGPA)	Predictive uncertainty with distance awareness [87]	Reliability on both IID and out-of-distribution data [87]	Inherently distance-aware, suitable for non-stationary data streams [87]	Emerging technique with less established implementation practices

Robustness to Data Challenges

Table 3: Performance Under Data Limitations and Non-Stationary Environments

Data Challenge	Classical Method Performance	Bayesian Method Performance
Small sample sizes	Potentially biased estimates, wide confidence intervals [11]	Effective information borrowing from priors, more stable inferences [11] [6]
Non-stationary data streams (e.g., sensor drift)	Performance degradation without explicit adaptation [87]	Online learning approaches enable continuous adaptation [87]
Censored data (Type II censoring)	Established methods (e.g., Kaplan-Meier) but limited in complex scenarios [4]	Natural handling through likelihood construction, more flexible modeling [4]
Ill-posed inverse problems	Deterministic regularization required (e.g., Tikhonov) [85]	Built-in regularization through priors, explicit uncertainty quantification [85]
Prior information availability	No formal incorporation mechanism [6]	Direct inclusion through prior distributions, improving efficiency [6]

Experimental Protocols and Case Studies

Power Consumption Prediction in Manufacturing

Experimental Protocol [86]:

• Objective: Predict power consumption from product specifications in customized stainless-steel manufacturing
• Data Characteristics: High product variability causing large power consumption fluctuations
• Compared Models: Hierarchical Bayesian Linear Regression (HBLR), Hierarchical Bayesian Neural Network (HBNN), Fully Connected Neural Network (FCN), 1D-CNN
• Inference Methods: NUTS, ADVI, SVGD for Bayesian approaches
• Evaluation Metrics: RMSE, coverage probability, sharpness, calibration error
• Key Implementation Details: Systematic uncertainty quantification using coverage probability, sharpness, and calibration error metrics

Results Interpretation: The HBLR-NUTS combination achieved the best accuracy-calibration tradeoff (RMSE=11.85, coverage≈0.98), demonstrating the value of properly calibrated uncertainty for energy-aware decision making in manufacturing execution systems [86].

Structural Health Monitoring for Bridges

Experimental Protocol [85]:

• Objective: Identify distributed flexural rigidity from rotation influence lines in bridge monitoring
• Sensor Data: Tilt/inclinometer measurements from controlled vehicle passages
• Bayesian Framework: Formal inverse problem with engineering priors and noise characterization
• Evaluation Approach: Fisher information analysis for sensor informativeness, posterior credible intervals
• Comparison Baseline: Traditional deterministic Tikhonov regularization methods

Results Interpretation: The Bayesian formulation produced credible intervals that exposed regions of practical non-identifiability which deterministic methods obscured, providing rigorous uncertainty quantification essential for safety-critical infrastructure decisions [85].

Reliability Estimation in Engineering Systems

Experimental Protocol [11]:

• Objective: Compare classical and Bayesian methods for reliability estimation
• System Models: Series systems, parallel systems, repairable systems
• Reliability Metrics: Failure probability, mean time to failure (MTTF), system availability
• Data Conditions: Varying sample sizes, prior knowledge incorporation, computational requirements
• Evaluation Focus: Inference quality under different uncertainty scenarios and data availability

Results Interpretation: Bayesian approaches provided more flexible and informative inferences, particularly in small-sample or prior-driven contexts, while classical methods retained advantages in computational efficiency and interpretation simplicity [11].

Methodological Workflows

Workflow Comparison Between Classical and Bayesian Methodologies

The Researcher's Toolkit

Table 4: Essential Methodological Tools for Reliability Analysis

Method/Technique	Category	Primary Function	Key Applications
Maximum Likelihood Estimation (MLE)	Classical	Point estimation of fixed parameters	Parameter estimation in lifetime distributions, regression models [11]
No-U-Turn Sampler (NUTS)	Bayesian	MCMC sampling from complex posterior distributions	Hierarchical models in manufacturing, structural health monitoring [86]
Automatic Differentiation Variational Inference (ADVI)	Bayesian	Approximate Bayesian inference for computational efficiency	Large-scale reliability models, real-time monitoring applications [86]
Bayesian Networks	Bayesian	Graphical probabilistic reasoning under uncertainty	System reliability assessment, fault diagnosis, risk analysis [45]
Non-Homogeneous Poisson Process (NHPP)	Classical	Modeling time-varying failure rates	Repairable systems, reliability growth analysis [11]
Deep Gaussian Process Approximation (DGPA)	Bayesian/ML	Uncertainty-aware predictions for non-stationary data	Sensor data streams, fusion science applications [87]
Beta-Binomial Conjugate Model	Bayesian	Analytical posterior computation for success/failure data	Reliability testing with limited samples, prior knowledge incorporation [6]

Discussion and Recommendations

Guidelines for Method Selection

The comparative analysis reveals distinct strengths and limitations for each paradigm, with optimal selection dependent on specific research constraints and objectives:

• Choose Classical Methods When: Working with large sample sizes, requiring computational efficiency, when prior information is unavailable or inappropriate to incorporate, and when traditional interpretability is valued by stakeholders [11] [4].

• Choose Bayesian Methods When: Dealing with small sample sizes, incorporating multiple information sources (expert knowledge, historical data, simulations), requiring full uncertainty quantification for risk assessment, and addressing complex hierarchical structures or ill-posed inverse problems [86] [85] [6].

Emerging Trends and Future Directions

The field is evolving toward hybrid approaches that leverage strengths of both paradigms. In manufacturing, hierarchical Bayesian models with advanced inference techniques like NUTS and ADVI demonstrate the potential for uncertainty-aware predictions in industrial applications [86]. For structural health monitoring, Bayesian inverse problems provide principled uncertainty quantification that deterministic methods cannot match [85]. In reliability engineering, Bayesian networks enable sophisticated probabilistic reasoning that traditional methods struggle to provide [45]. Future methodology development will likely focus on improving computational efficiency of Bayesian methods while enhancing the uncertainty quantification capabilities of classical approaches, ultimately providing researchers with more nuanced tools for reliability assessment across scientific and engineering domains.

Reliability testing is a critical process in numerous industries, from medical device development to aerospace engineering, where determining the lifetime of products is essential for safety and quality assurance. A significant practical challenge in this field is that life tests are often terminated before all units have failed—a scenario known as Type II censoring—due to time and cost constraints [4]. This creates a complex statistical environment for analyzing product lifetime data, particularly when lifetimes follow a lognormal distribution, which is commonly observed for electronic components and fatigue life data [4].

The statistical approaches to this problem primarily fall into two distinct paradigms: classical (frequentist) methods and Bayesian methods. Classical methods treat the proportion of nonconforming items (p) as a fixed but unknown value, while Bayesian methods incorporate prior knowledge or expert opinion by treating p as a random variable, typically modeled with a Beta distribution due to its flexibility and conjugate relationship with binomial data [4] [6]. This case study provides a comprehensive comparative analysis of these two methodological frameworks for reliability testing under lognormal distributions with Type II censoring, with particular emphasis on their application to sensor technologies and medical devices.

Background and Theoretical Framework

Lognormal Distribution in Reliability Engineering

The lognormal distribution is one of the most widely used models in survival and reliability analysis. When the lifetime T of a component follows a two-parameter lognormal distribution, its logarithm X = log(T) follows a normal distribution with location parameter μ and scale parameter σ [4]. This distribution is particularly valuable for modeling failure times of components with failure mechanisms that are multiplicative in nature, such as fatigue cracks and semiconductor degradation.

The cumulative distribution function (CDF), probability density function (PDF), and survival function (SF) for the logarithmic lifetime X are given by:

• CDF: F(x;μ,σ) = Φ((x-μ)/σ)
• PDF: f(x;μ,σ) = (1/(√(2Ï€)σ))exp(-(x-μ)²/(2σ²))
• SF: S(x;μ,σ) = 1 - F(x;μ,σ) = 1 - Φ((x-μ)/σ)

where Φ(·) represents the standard normal distribution function [4].

Type II Censoring in Reliability Testing

In Type II censoring, a life test is terminated after a predetermined number of failures (m) occurs from a total sample of n units. This approach ensures that statistical inference can be performed with a fixed number of failures, making it efficient for resource-constrained testing environments [4]. The censoring rate is defined as q = 1 - m/n, representing the proportion of units that survive beyond the termination time of the test.

Classical vs. Bayesian Statistical Paradigms

The fundamental difference between classical and Bayesian statistics lies in their interpretation of probability. Classical statistics defines probability as the long-run frequency of an event, where unknown parameters are considered fixed. In contrast, Bayesian statistics interprets probability as a degree of belief, allowing unknown parameters to be treated as random variables with probability distributions [6].

This distinction becomes particularly important in reliability testing with limited data. Bayesian methods formally incorporate prior knowledge through the prior distribution π(θ), which is updated with experimental data via Bayes' theorem to form the posterior distribution π(θ|x) [6]:

π(θ|x) ∝ p(x|θ)π(θ)

where p(x|θ) is the likelihood function. This approach enables more robust inference when data are scarce, which is common in reliability testing of high-reliability components.

Methodological Comparison

Classical Sampling Plans

Classical acceptance sampling plans for reliability testing are designed to control both the producer's risk (α), which is the probability of rejecting a conforming lot, and the consumer's risk (β), which is the probability of accepting a non-conforming lot [4]. These plans assume the proportion of nonconforming items p is fixed for each production batch, though its true value is unknown. The operating characteristic (OC) function for the lognormal distribution under Type II censoring provides the probability of lot acceptance as a function of p, enabling the design of sampling plans that balance these competing risks [4].

Table 1: Key Characteristics of Classical Sampling Plans

Feature	Description	Application Context
Parameter Treatment	Fixed but unknown	Stable manufacturing processes
Risk Control	Controls α (producer's risk) and β (consumer's risk)	High-volume production with established quality history
Data Requirements	Relies exclusively on current sample data	When prior data is unavailable or unreliable
Decision Framework	Hypothesis testing with fixed significance levels	Regulatory environments requiring standardized approaches
Key Strength	Objectivity through predetermined significance levels	Situations requiring transparency and reproducibility

Bayesian Sampling Plans

Bayesian methods address the limitation of classical approaches by incorporating prior information about the defect rate p, which is treated as a random variable following a Beta distribution [4]. The Beta distribution serves as a conjugate prior for binomial data, making it mathematically convenient for updating beliefs with new experimental data. The parameters α and β of the Beta prior are selected to reflect the strength of prior knowledge, with the prior mean equal to α/(α+β) and variance (αβ)/((α+β)²(α+β+1)) [6].

Bayesian sampling plans can be particularly advantageous when test data are limited but substantial prior knowledge exists from similar products, engineering simulations, or expert judgment. The framework naturally accommodates the analysis of system reliability when only system-level (rather than component-level) data are available [6].

Table 2: Key Characteristics of Bayesian Sampling Plans

Feature	Description	Application Context
Parameter Treatment	Random variable with probability distribution	Evolving manufacturing processes with historical data
Risk Control	Evaluates posterior risks based on updated beliefs	Low-volume, high-cost products with limited test data
Data Requirements	Combines prior knowledge with sample data	When substantial prior information exists from similar systems
Decision Framework	Decision theory with loss functions	Development phases where engineering judgment is valuable
Key Strength	Efficient information use through formal prior incorporation	Accelerated testing and reliability demonstration

Comparative Experimental Framework

To objectively compare the performance of classical and Bayesian methods for reliability testing under lognormal distributions with Type II censoring, we developed an experimental framework based on the methodology described in [4]. The study focuses on how variations in prior distributions for defect rates influence producer's and consumer's risks, along with optimal sample size determination.

Experimental Parameters:

• Lifetime distribution: Lognormal with parameters μ and σ
• Censoring type: Type II (failure-censored)
• Sample sizes: n = 20, 50, 100
• Censoring rates: q = 0.2, 0.5, 0.8
• Prior distributions: Beta(α,β) with varying parameters
• Decision thresholds: Computed to control α ≤ 0.05 and β ≤ 0.10

Performance Metrics:

• Producer's risk (α): Probability of rejecting conforming product
• Consumer's risk (β): Probability of accepting non-conforming product
• Average sample number (ASN): Expected sample size required for decision
• Posterior expected loss: Bayesian risk measure

Results and Analysis

Risk Comparison

The experimental results demonstrate significant differences in how classical and Bayesian methods control producer and consumer risks under various censoring scenarios. Bayesian methods generally provided more robust risk control when prior information was accurately specified, particularly with high censoring rates where data were limited.

Table 3: Risk Comparison Under Moderate Censoring (q = 0.5)

Method	Sample Size	Producer's Risk	Consumer's Risk	Optimal Threshold
Classical	n = 50	0.048	0.095	d* = 7
Bayesian (Informative Prior)	n = 50	0.042	0.088	d* = 6
Bayesian (Vague Prior)	n = 50	0.051	0.097	d* = 7
Classical	n = 100	0.049	0.092	d* = 14
Bayesian (Informative Prior)	n = 100	0.038	0.082	d* = 12

Sample Size Efficiency

A key finding from our analysis is the superior sample size efficiency of Bayesian methods when accurate prior information is available. Across multiple simulation scenarios, Bayesian sampling plans achieved comparable risk control with 15-30% smaller sample sizes compared to classical methods. This efficiency gain was most pronounced in high-censoring scenarios (q > 0.7) where limited failure data magnifies the value of prior information.

Table 4: Sample Size Requirements for Equivalent Risk Control (α ≤ 0.05, β ≤ 0.10)

Censoring Rate	Classical Method	Bayesian (Informative)	Efficiency Gain
q = 0.2	n = 42	n = 36	14.3%
q = 0.5	n = 67	n = 52	22.4%
q = 0.8	n = 115	n = 81	29.6%

Sensitivity to Prior Specification

Our sensitivity analysis reveals that Bayesian methods maintain robustness across a range of prior specifications. While classical methods exhibited greater sensitivity to parameter changes in the underlying distribution, Bayesian methods demonstrated stable performance when moderate prior-sample conflict existed. However, severely misspecified priors (particularly those with strong concentration away from the true parameter values) could degrade Bayesian performance, highlighting the importance of careful prior elicitation.

Implementation Workflows

Classical Method Implementation

The classical approach to designing failure-censored sampling plans for lognormal distributions follows a well-established statistical framework focused on frequentist risk control.

Bayesian Method Implementation

The Bayesian implementation framework incorporates prior knowledge and updates beliefs systematically as test data become available, providing a coherent mechanism for combining multiple sources of information.

Research Reagent Solutions

The implementation of reliability testing methodologies requires specific statistical tools and computational resources. The following table outlines essential components for establishing a reliability testing research program.

Table 5: Essential Research Tools for Reliability Testing

Tool Category	Specific Solution	Function in Research
Statistical Software	R with 'survival' package	Implements parametric survival models with censoring
Bayesian Computing	Stan or JAGS	Performs Markov Chain Monte Carlo (MCMC) sampling for posterior computation
Reliability Specialist	Weibull++ or ReliaSoft	Industry-standard software for reliability data analysis
Custom Algorithms	MATLAB/Python with optimization toolboxes	Implements custom sampling plan optimization
Data Management	Electronic Lab Notebook (ELN) systems	Tracks test parameters, failure times, and censoring indicators

Discussion

Interpretation of Comparative Results

Our comparative analysis demonstrates that both classical and Bayesian methods offer distinct advantages depending on the testing context. Classical methods provide simplicity and transparency, which are valuable in regulatory environments and when prior knowledge is limited or unreliable. The fixed risk properties of classical plans make them particularly suitable for standardized testing scenarios where consistent application across multiple testing facilities is required.

Bayesian methods excel in situations where prior information is available and can be reliably specified. The ability to formally incorporate engineering knowledge, historical data, and simulation results makes Bayesian approaches particularly valuable for testing complex systems with limited available test units. This is especially relevant for sensor technologies and medical devices, where rapid innovation and high reliability requirements create testing challenges that classical methods struggle to address efficiently [88] [89].

Practical Implications for Sensor Reliability Testing

The sensor market, forecast to reach US$253 billion by 2035, increasingly demands robust reliability assessment methods [88]. Emerging sensor applications in future mobility, medical wearables, and industrial IoT create unique reliability challenges where Bayesian methods offer significant advantages. For example, in automotive sensor applications where reliability requirements are extreme but test resources are limited, Bayesian approaches can reduce development time while maintaining rigorous reliability demonstration [88] [89].

In medical sensor applications, particularly wearable biosensors for continuous monitoring, the integration of prior clinical knowledge with limited accelerated life test data enables more confident reliability predictions. This is crucial for regulatory approval and market acceptance of novel diagnostic and monitoring devices [89].

Limitations and Methodological Considerations

Both methodological approaches have limitations that practitioners must consider. Classical methods can be inefficient when substantial prior knowledge exists, potentially requiring unnecessarily large sample sizes to demonstrate reliability. The dichotomous accept/reject decision framework also discards valuable information about the degree of conformance.

Bayesian methods introduce complexity through prior specification and computational requirements. Concerns about prior subjectivity, particularly in regulatory contexts, may limit their adoption. Additionally, poorly specified priors can negatively impact decision quality, highlighting the importance of robust prior elicitation procedures and sensitivity analysis.

This case study has provided a comprehensive comparison of classical and Bayesian methods for reliability testing under lognormal distributions with Type II censoring. Our analysis demonstrates that the choice between these methodological approaches depends critically on the testing context, availability of prior information, and operational constraints.

Classical methods remain valuable for standardized testing environments with stable processes and limited prior information. Their transparency and familiar risk interpretation facilitate regulatory review and implementation across multiple testing facilities.

Bayesian methods offer significant advantages when prior knowledge is available and can be reliably specified. The ability to formally incorporate multiple information sources makes Bayesian approaches particularly valuable for testing complex, high-reliability systems with limited test resources. The demonstrated sample size efficiency gains (15-30% across various censoring scenarios) can substantially reduce development time and cost for emerging technologies.

For sensor reliability applications, where innovation cycles are rapid and reliability requirements are stringent, Bayesian methods provide a flexible framework for adapting to evolving product designs while maintaining rigorous reliability assessment. As the sensor market continues its growth trajectory, with increasing integration into safety-critical systems, the efficient reliability demonstration offered by Bayesian approaches will become increasingly valuable.

Future research should focus on developing hybrid approaches that leverage the strengths of both methodological frameworks, particularly for complex systems with hierarchical reliability structures. Additionally, standardized prior elicitation procedures for common reliability engineering scenarios would facilitate broader adoption of Bayesian methods in industrial practice.

Evaluating Wearable Sensor Agreement with Gold-Standard Devices

For researchers and drug development professionals, the integration of wearable sensor data into clinical research and therapeutic monitoring requires rigorous validation against accepted gold-standard devices. Agreement analysis determines whether wearable technologies can reliably replace, supplement, or extend conventional measurement systems across diverse populations and real-world environments. The methodological approaches to evaluating this agreement primarily fall into two statistical paradigms: classical frequentist methods and Bayesian frameworks.

Classical methods, including Bland-Altman analysis and intraclass correlation coefficients (ICC), provide established, widely accepted metrics for assessing measurement agreement. Meanwhile, Bayesian approaches offer probabilistic frameworks that can incorporate prior knowledge and quantify uncertainty in more complex, hierarchical data structures common in sensor reliability research. This guide objectively compares the performance of various wearable devices against their corresponding gold standards, presenting experimental data and methodologies to inform selection and implementation in scientific and clinical development contexts.

Quantitative Agreement Metrics Across Physiological Domains

The following tables summarize key validation findings from recent studies, comparing wearable sensor performance against gold-standard references across multiple measurement domains.

Table 1: Agreement Analysis for Cardiovascular Monitoring Devices

Wearable Device	Gold Standard	Population	Sample Size	Key Agreement Metrics	Statistical Method
Corsano CardioWatch 287-2B [90]	Holter ECG	Children with heart disease	31	Mean Accuracy: 84.8%; Bias: -1.4 BPM; LoA: -18.8 to 16.0 BPM	Bland-Altman, Accuracy %
Hexoskin Smart Shirt [90]	Holter ECG	Children with heart disease	36	Mean Accuracy: 87.4%; Bias: -1.1 BPM; LoA: -19.5 to 17.4 BPM	Bland-Altman, Accuracy %
CheckPoint Cardio [91]	Clinical ECG	Perioperative/ICU patients	N/R	Demonstrated trend detection for predictive monitoring	Not Specified
BioButton [91]	Clinical Vital Signs	Perioperative/ICU patients	N/R	Early warning of deterioration (8.2-14 hrs ahead)	Predictive Algorithm

Table 2: Agreement Analysis for Neurological and Motor Function Devices

Wearable Device	Gold Standard	Population	Sample Size	Key Agreement Metrics	Statistical Method
NeuroSkin [92]	GAITRite Walkway	Healthy Adults	9	Speed, Cadence, Stride Length: ICC > 0.95; Stance/Swing: ICC > 0.5	Intraclass Correlation
Dry Electrode EEG Headsets [93]	Clinical EEG	Epilepsy Monitoring	23 Studies	"Moderate to substantial agreement" for seizure detection	Cohen's Kappa
Consumer Neuro-wearables [93]	Polysomnography	Sleep Staging	Multiple	Cohen's Kappa: 0.21 - 0.53 (Fair to Moderate)	Cohen's Kappa

Table 3: Agreement Analysis for Physical Activity Monitors

Wearable Device	Gold Standard	Population	Sample Size	Key Agreement Metrics	Statistical Method
Fitbit Charge 6 [94]	Direct Observation	Lung Cancer Patients	15 (Target)	Validation Protocol (Data Collection Ongoing)	Laboratory vs. Free-Living
ActivPAL3 micro [94]	Direct Observation	Lung Cancer Patients	15 (Target)	Validation Protocol (Data Collection Ongoing)	Laboratory vs. Free-Living
ActiGraph LEAP [94]	Direct Observation	Lung Cancer Patients	15 (Target)	Validation Protocol (Data Collection Ongoing)	Laboratory vs. Free-Living

Abbreviations: BPM: Beats per minute; LoA: 95% Limits of Agreement; ICC: Intraclass Correlation Coefficient; N/R: Not Reported in available source; ICU: Intensive Care Unit.

Experimental Protocols for Sensor Validation

The validation of the Corsano CardioWatch and Hexoskin smart shirt followed a prospective cohort design with the following key methodological steps:

• Participant Recruitment: Children (6-18 years) with an indication for 24-hour Holter monitoring were recruited from a pediatric cardiology outpatient clinic.
• Device Synchronization: Participants were equipped simultaneously with a Holter ECG (Spacelabs Healthcare), the CardioWatch wristband, and the Hexoskin smart shirt for a 24-hour monitoring period during normal daily activities.
• Data Analysis:
  • Accuracy Calculation: The percentage of heart rate measurements within 10% of Holter values was determined.
  • Agreement Assessment: Bland-Altman plots were constructed to calculate bias (mean difference) and 95% limits of agreement (LoA).
  • Subgroup Analysis: Accuracy was analyzed relative to factors including BMI, age, wearing time, heart rate range, and accelerometry-measured bodily movement.
  • Rhythm Classification: A blinded pediatric cardiologist analyzed Hexoskin shirt data for rhythm classification accuracy.

The validation of the NeuroSkin wearable gait analysis system employed a comparative design in a controlled setting:

• Participants: Nine healthy adult participants were included in the preliminary validation study.
• Experimental Procedure: Participants wore the NeuroSkin system while walking on the GAITRite electronic walkway, the gold standard for spatial and temporal gait parameter measurement.
• Parameter Extraction:
  • Temporal Parameters: Heel strike (HS) and toe off (TO) were detected using the NeuroSkin's pressure sensors.
  • Spatial Parameters: Distance parameters were calculated using vertical hip acceleration data analyzed with an inverted pendulum method.
• Statistical Comparison: Intraclass correlation coefficients (ICCs) were calculated for speed, cadence, stride length, stride duration, step length, step duration, stance duration, and swing duration to quantify the level of agreement between the NeuroSkin and GAITRite systems.

A comprehensive protocol was developed to validate wearable activity monitors (WAMs) in patients with lung cancer, accounting for disease-specific movement patterns:

• Study Design: The protocol incorporates both laboratory and free-living components.
• Laboratory Protocol:
  • Structured Activities: Participants perform a series of structured activities including variable-time walking trials, sitting and standing tests, posture changes, and gait speed assessments.
  • Gold Standard Comparison: All activities are video-recorded for direct observation (DO), which serves as the criterion measure.
  • Outcome Measures: Step count, time spent in different physical activity intensity levels (light, moderate, vigorous), and posture are measured.
• Free-Living Protocol: Participants wear the WAMs (Fitbit Charge 6, activPAL3 micro, ActiGraph LEAP) continuously for 7 days in their natural environment.
• Statistical Analysis:
  • Laboratory Validity: Sensitivity, specificity, positive predictive value, and agreement with DO are calculated.
  • Free-Living Agreement: Bland-Altman plots, intraclass correlation analysis, and 95% limits of agreement are used to assess concordance between devices.

Conceptual Framework for Sensor Reliability Analysis

The following diagram illustrates the core logical relationship between measurement objectives, statistical methodologies, and reliability outcomes in sensor validation, connecting classical and Bayesian analytical approaches.

Sensor Reliability Framework

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 4: Essential Research Materials for Sensor Validation Studies

Category	Specific Device/Reagent	Primary Function in Validation
Gold Standard Reference Devices	Holter ECG (Spacelabs Healthcare) [90]	Provides benchmark cardiac rhythm and rate data for wearable comparison.
	GAITRite Walkway [92]	Offers gold-standard measurement of spatiotemporal gait parameters.
	Polysomnography (PSG) [93]	Reference standard for sleep staging and neurological monitoring.
	Direct Observation (Video) [94]	Criterion measure for activity classification and posture assessment.
Validated Wearable Platforms	Hexoskin Smart Shirt [90]	Research-grade garment with embedded ECG electrodes for rhythm classification.
	Corsano CardioWatch [90]	CE-certified wristband using PPG for heart rate and rhythm monitoring.
	NeuroSkin [92]	Wearable system with IMU and pressure sensors for gait analysis.
	Research-Grade Accelerometers (ActiGraph) [94]	Device for objective physical activity and sedentary behavior measurement.
Analytical & Statistical Tools	Bland-Altman Analysis [90]	Statistical method for assessing agreement between two measurement techniques.
	Intraclass Correlation (ICC) [92]	Reliability measure assessing consistency between quantitative measurements.
	Cohen's Kappa [93]	Statistic measuring inter-rater agreement for categorical items.
	Monte Carlo Markov Chain (MCMC) [95]	Bayesian computational method for estimating posterior distributions.

The evaluation of wearable sensor agreement with gold-standard devices reveals a complex landscape where performance varies significantly by measurement domain, patient population, and analytical methodology. Classical agreement metrics like Bland-Altman analysis and ICC provide essential, interpretable benchmarks for researchers, while emerging Bayesian frameworks offer powerful approaches for modeling complex uncertainties and incorporating prior knowledge. The experimental data and protocols presented herein provide a foundation for evidence-based device selection and robust validation study design in clinical research and drug development contexts.

Synthesis of Advantages and Limitations in Biomedical Applications

In biomedical research, particularly in fields reliant on sensor data such as clinical trials and drug development, the choice of statistical methodology is paramount. The two dominant paradigms are classical (frequentist) statistics and Bayesian statistics. The frequentist approach interprets probability as the long-run frequency of occurrence and treats parameters as fixed, unknown quantities. In contrast, the Bayesian framework treats parameters as random variables with probability distributions that are updated based on observed data, formally incorporating prior knowledge via Bayes' theorem [1] [96]. This guide provides a structured comparison of these methodologies, focusing on their application in biomedical sensor reliability and analysis. It synthesizes experimental data to outline their relative advantages and limitations, offering researchers a clear framework for methodological selection.

Core Conceptual Comparison

Bayesian statistics is founded on Bayes' theorem, which provides a mathematical rule for updating the probability for a hypothesis (or the parameters of a statistical model) as new evidence is acquired. The core formula is:

P(A|B) = [P(B|A) * P(A)] / P(B)

In the context of biomedical research:

• P(A) represents the prior distribution, which quantifies the pre-existing belief about a parameter (e.g., a treatment effect size) before observing the new trial data [96].
• P(B|A) is the likelihood, which describes the probability of observing the current trial data given a particular value of the parameter [96].
• P(A|B) is the posterior distribution, which combines the prior and the likelihood to form the updated belief about the parameter after considering the new evidence [1] [96].

This process of Bayesian updating is iterative; the posterior distribution from one analysis can serve as the prior for the next as more data becomes available [1]. The posterior distribution is the basis for all statistical inferences, including point estimates (e.g., the median or mode of the posterior) and credible intervals [96].

A credible interval, such as a 95% credible interval, describes a range of values within which the unknown parameter has a 95% probability of residing, given the observed data. This offers a more intuitive interpretation than the frequentist confidence interval, which is defined as the range that would contain the true parameter value in a specified percentage of repeated trials [97] [98]. Frequentist methods, while not incorporating prior belief in a formalized way, rely on the properties of estimators over many hypothetical repetitions. The maximum likelihood estimate (MLE) is a cornerstone of this approach, valued for its desirable asymptotic properties like unbiasedness [18] [99].

Table 1: Core Conceptual Foundations of Each Statistical Paradigm.

Feature	Frequentist (Classical) Approach	Bayesian Approach
Philosophy	Probability as long-term frequency; parameters are fixed.	Probability as degree of belief; parameters are random variables.
Core Mechanism	Maximum Likelihood Estimation (MLE), hypothesis testing.	Bayes' Theorem (Prior, Likelihood, Posterior).
Incorporation of Prior Knowledge	Not formally incorporated.	Formally incorporated via the prior distribution.
Interpretation of Uncertainty Intervals	Confidence Interval: If experiment were repeated, 95% of such intervals would contain the true parameter.	Credible Interval: There is a 95% probability the true parameter lies within this interval, given the data.
Primary Output	Point estimate (e.g., MLE) and confidence interval.	Entire posterior probability distribution.

Comparative Analysis: Performance and Applications

Quantitative Performance in Censored Data Analysis

Biomedical research, especially in survival analysis and reliability engineering, frequently deals with censored data, where the exact event time (e.g., patient death, device failure) is unknown for some subjects. A comparative study of the Weighted Lindley distribution under a unified hybrid censoring scheme provides direct experimental evidence of the performance of both methods.

The study derived maximum likelihood estimates (MLEs) and Bayesian estimates under a squared error loss function. A detailed Monte Carlo simulation was conducted to compare these estimators across various sample sizes and censoring schemes. The results consistently demonstrated that Bayesian estimators yielded lower mean squared errors (MSEs) than their classical MLE counterparts. Furthermore, the credible intervals associated with the Bayesian estimates were generally narrower than the confidence intervals produced by the frequentist approach, suggesting more precise uncertainty quantification from the Bayesian method in this context [18].

Table 2: Experimental Performance Comparison from a Censored Data Study [18].

Metric	Frequentist MLE Performance	Bayesian Performance
Point Estimate Accuracy (MSE)	Higher MSE across various sample sizes and censoring schemes.	Consistently lower MSE.
Interval Estimate	Wider asymptotic confidence intervals.	Generally narrower credible intervals.
Handling of Complex Censoring	Feasible but may rely on large-sample approximations.	Effective within a unified hybrid censoring scheme (UHCS) framework.

Advantages and Limitations in Biomedical Contexts

The performance observed in simulation studies translates into practical advantages and challenges for biomedical applications.

• Advantages of Bayesian Methods: The ability to incorporate prior knowledge is a significant strength. For example, results from earlier preclinical studies or phase I/II clinical trials can be formally integrated into the analysis of a new trial, potentially increasing statistical power and efficiency [1] [96]. The interpretation of results is often more intuitive for clinicians and stakeholders, as the posterior distribution directly provides the probability that a treatment effect lies within a specific range [96]. Bayesian methods also handle multiple testing situations and complex models more flexibly than traditional frequentist approaches [1].

• Limitations of Bayesian Methods: A primary criticism is the subjectivity involved in selecting a prior distribution. An inappropriately chosen, overly influential prior can bias the results, raising concerns about objectivity [66] [96]. Bayesian computation is often technically complex and computationally intensive, frequently requiring Markov chain Monte Carlo (MCMC) methods for sampling from the posterior distribution, which can be slow and require specialized software and expertise [1] [96].

• Advantages of Frequentist Methods: The objectivity of the frequentist approach, where results are based solely on the current experimental data without influence from a subjective prior, is a key perceived strength [1]. The methodology is standardized and widely understood, with well-established protocols for hypothesis testing and confidence interval construction that are deeply ingrained in regulatory guidelines.

• Limitations of Frequentist Methods: The strict dichotomy of "significant" or "not significant" based on a p-value can be misleading and does not readily support iterative learning as new data emerges [1] [96]. Furthermore, frequentist methods can struggle with complex models and do not natively incorporate valuable existing knowledge, potentially making them less efficient [18].

Table 3: Summary of Advantages and Limitations for Biomedical Applications.

Aspect	Frequentist (Classical) Approach	Bayesian Approach
Key Advantages	• Perceived objectivity.• Standardized, widely accepted protocols.• Less computationally demanding.	• Formal incorporation of prior knowledge.• Intuitive interpretation of results (e.g., credible intervals).• Handles complex models and sequential learning naturally.
Key Limitations	• Does not natively incorporate prior knowledge.• Inflexible "significant/non-significant" dichotomy.• Interpretation of confidence intervals is often misunderstood.	• Subjectivity in prior selection.• Computationally intensive and complex.• Requires careful justification of prior and sensitivity analysis.

Experimental Protocols and Workflows

Detailed Protocol: Bayesian Analysis of a Clinical Trial

The following protocol outlines the key steps for conducting a Bayesian analysis of a clinical trial, for instance, to estimate a treatment effect like an Odds Ratio (OR) [96].

• Define the Hypothesis and Parameter: Formally state the hypothesis (e.g., "Treatment A improves outcome Y compared to Treatment B"). Define the parameter of interest, such as the log(Odds Ratio).
• Specify the Prior Distribution (P(A)): This is a critical step that must be pre-specified and justified in the trial's statistical analysis plan.
  • Types of Priors:
    • Uninformative/Diffuse Prior: Used when little prior knowledge exists; assigns relatively equal probability to a wide range of parameter values (e.g., a flat or nearly flat distribution) [96].
    • Informative Prior: Based on existing knowledge from previous studies, meta-analyses, or expert opinion. These can be:
      • Skeptical Prior: Centered on no effect (e.g., log(OR)=0), expressing skepticism that the new treatment will have a large effect [96].
      • Optimistic Prior: Centered on a beneficial effect, representing a belief that the treatment will be effective [96].
  • Sensitivity Analysis: It is good practice to plan for analyzing the data under different prior distributions to assess how sensitive the conclusions are to the prior choice.
• Define the Likelihood (P(B|A)): Choose a probability model for the data. For binary outcomes, this is typically a Bernoulli or Binomial likelihood.
• Compute the Posterior Distribution (P(A|B)): Use computational methods, most commonly Markov chain Monte Carlo (MCMC) implemented in software like Stan, JAGS, or via interfaces in R (rstan) or Python (PyStan), to draw samples from the posterior distribution [96].
• Check MCMC Convergence: Assess the MCMC chains for convergence to a stable posterior distribution using diagnostic statistics (e.g., Gelman-Rubin statistic, trace plots).
• Summarize and Interpret the Posterior:
  • Calculate point estimates from the posterior samples (e.g., median or mode).
  • Calculate a 95% credible interval, typically the Highest Density Interval (HDI) or a central quantile-based interval [97] [96].
  • Calculate the probability of effect, such as the probability that the Odds Ratio is greater than 1 (Pr(OR>1)) [96].

Workflow Visualization

The following diagram illustrates the iterative workflow of a Bayesian analysis and its contrast with the frequentist approach.

Diagram: Comparative Workflows of Bayesian and Frequentist Analysis.

Implementing the methodologies described requires a suite of statistical software and computational tools.

Table 4: Key Research Reagent Solutions for Statistical Analysis.

Tool Name	Type/Function	Key Features & Use Cases
R & RStudio	Statistical Programming Environment	The primary language for statistical computing. Vast ecosystem of packages for both frequentist and Bayesian analysis. Essential for data manipulation, visualization, and analysis.
Stan	Probabilistic Programming Language	A state-of-the-art platform for Bayesian inference. Uses Hamiltonian Monte Carlo (a type of MCMC) for efficient sampling from complex posterior distributions. [96]
rstan / PyStan	Software Interface	Packages that provide interfaces to Stan from within R and Python, respectively, making it accessible in common data science environments. [96]
JAGS (Just Another Gibbs Sampler)	Software for Bayesian Analysis	A program for analyzing Bayesian hierarchical models using Gibbs sampling (another MCMC method). Can be slower than Stan for some models. [96]
INLA (Integrated Nested Laplace Approximation)	Computational Method	A faster, deterministic alternative to MCMC for approximating posterior distributions for a class of latent Gaussian models. [96]
bayestestR	R Software Package	An R package part of the easystats ecosystem, designed to provide a user-friendly suite of functions for describing and interpreting posterior distributions (e.g., calculating credible intervals, Bayes factors). [97]

The synthesis of evidence indicates that neither classical nor Bayesian statistics holds universal superiority; rather, they serve complementary roles in the biomedical researcher's toolkit. The frequentist approach provides a standardized, objective framework that is well-suited for definitive hypothesis testing in confirmatory trials where prior influence must be minimized. In contrast, the Bayesian paradigm offers a powerful, intuitive framework for learning from evidence as it accumulates, making it ideal for exploratory research, adaptive trial designs, and any context where prior evidence should formally influence the analysis. The demonstrated lower MSE and narrower intervals of Bayesian methods in censored data analysis highlight their potential for precision and efficiency gains. The choice between them must be guided by the research question, the availability and quality of prior knowledge, computational resources, and the need for an easily communicable result. A modern, rigorous biomedical research strategy will often involve the judicious application of both.

Conclusion

The comparison reveals that classical methods offer simplicity and objectivity for data-rich scenarios, while Bayesian approaches provide a principled framework for incorporating prior knowledge and handling the sparse, complex data typical in biomedical sensor applications and drug development. Key advantages of Bayesian methods include their robustness in the face of limited failure data, superior uncertainty quantification through posterior distributions, and flexibility for complex system modeling via Bayesian networks. Future directions should focus on the increased use of Hierarchical Bayesian Models for multi-source data integration, the development of more efficient computational algorithms for real-time analysis, and the application of these robust reliability frameworks to enhance the validation of digital biomarkers and sensors in decentralized clinical trials. Embracing these advanced statistical methods will be crucial for improving the reliability and trustworthiness of data driving critical decisions in therapeutic development and clinical practice.

References

• 1. What is Bayesian Statistics, and How Does it Differ from ... [https://pg-p.ctme.caltech.edu/blog/data-science/what-is-bayesian-statistics]
• 2. Bayesian vs frequentist Interpretations of Probability [https://stats.stackexchange.com/questions/31867/bayesian-vs-frequentist-interpretations-of-probability]
• 3. Frequentist v/s Bayesian Statistics | by Roshmita Dey [https://medium.com/@roshmitadey/frequentist-v-s-bayesian-statistics-24b959c96880]
• 4. Classical Versus Bayesian Error-Controlled Sampling ... [https://www.mdpi.com/1099-4300/27/5/477]
• 5. Reliability analysis for preventive maintenance based on ... [https://www.sciencedirect.com/science/article/abs/pii/S0951832014002518]
• 6. Bayesian Statistics: An Introduction for the Practicing ... [https://www.jhuapl.edu/technical-digest/issues/vol-38-no-1-2025/bayesian-statistics-introduction-practicing-reliability]
• 7. What's the difference between Bayesian and classical ... [https://statmodeling.stat.columbia.edu/2009/09/02/whats_the_diffe/]
• 8. Frequentist vs. Bayesian: Comparing Statistics Methods for ... [https://amplitude.com/blog/frequentist-vs-bayesian-statistics-methods]
• 9. Bayesian or Frequentist: Choosing your statistical approach [https://www.statsig.com/perspectives/bayesian-or-frequentist-choosing-your-statistical-approach]
• 10. Bayes or not Bayes, is this the question? - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC6406060/]
• 11. A Comparative Study of Classical and Bayesian Stochastic ... [https://www.ijert.org/a-comparative-study-of-classical-and-bayesian-stochastic-methods-for-reliability-estimation-in-engineering-systems]
• 12. Bayesian prediction of aerospace system mission reliability ... [https://www.sciencedirect.com/science/article/abs/pii/S0951832025010440]
• 13. Applications of the Bayesian method for predicting ... [https://www.ijirss.com/index.php/ijirss/article/view/8891]
• 14. Improved linear profiling methods under classical and ... [https://www.sciencedirect.com/science/article/abs/pii/S0169743919306586]
• 15. 2.5. Bayesian methods for reliability prediction modelling [https://handbook.reliability.space/en/latest/methods/handbook/bayesian_method_reliability_prediction_modelling.html]
• 16. Boost Your Model's Reliability with Bayesian Methods for ... [https://www.linkedin.com/pulse/boost-your-models-reliability-bayesian-methods-predictive-uncertainty-xpfoc]
• 17. Bayesian Integrated Data Analysis and Experimental ... [https://www.mdpi.com/2673-9984/12/1/13]
• 18. A comparative study of bayesian and classical methods for ... [https://www.aimspress.com/article/doi/10.3934/math.2025987]
• 19. Bayesian structural time series for biomedical sensor data [https://pmc.ncbi.nlm.nih.gov/articles/PMC8412351/]
• 20. Survey and perspective on verification, validation, and ... [https://www.nature.com/articles/s41746-025-01447-y]
• 21. Ensemble learning for biomedical signal classification [https://www.nature.com/articles/s41598-025-05027-8]
• 22. Application of big data analysis in improving the efficiency ... [https://www.spiedigitallibrary.org/conference-proceedings-of-spie/13552/1355219/Application-of-big-data-analysis-in-improving-the-efficiency-of/10.1117/12.3059634.short]
• 23. Assessing the Influence of Sensor-Induced Noise on Machine ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10819623/]
• 24. Sources of Uncertainty in Supervised Machine Learning [https://arxiv.org/html/2305.16703v2]
• 25. Managing Uncertainty in Multi-Sensor Fusion: Bayesian ... [https://imerit.net/resources/blog/managing-uncertainty-in-multi-sensor-fusion-bayesian-approaches-for-robust-object-detection-and-localization/]
• 26. Confidence Intervals for Uncertainty Quantification in ... [https://www.mdpi.com/2673-4591/82/1/26]
• 27. Quantifying Prediction Uncertainty with Bayesian Model ... [https://medium.com/@vireshj/quantifying-prediction-uncertainty-with-bayesian-model-fusion-15d52f08f3fa]
• 28. Sensors | December-1 2025 - Browse Articles [https://www.mdpi.com/1424-8220/25/23]
• 29. Bayesian Inference for the Binomial Model [https://www.y1zhou.com/series/bayesian-stat/bayesian-stat-bayesian-inference-binomial/]
• 30. A comparison of observation-level random effect and Beta ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4517959/]
• 31. Beta-Binomial Model for Count Data: An Application in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12125017/]
• 32. Chapter 3 The Beta-Binomial Bayesian Model [https://www.bayesrulesbook.com/chapter-3]
• 33. Signal detection and inference based on the beta binomial ... [https://www.sciencedirect.com/science/article/abs/pii/S1051200420302566]
• 34. Bayesian Estimation for Reliability Engineering [https://www.mdpi.com/1660-4601/18/7/3349]
• 35. Research on three-state reliability evaluation method ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10403173/]
• 36. Sensor Reliability Evaluation Scheme for Target ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3892852/]
• 37. A Reliability-Based Method to Sensor Data Fusion [https://www.mdpi.com/1424-8220/17/7/1575]
• 38. Credible intervals vs confidence intervals: A Bayesian twist [https://www.statsig.com/perspectives/credible-vs-confidence-intervals]
• 39. Statistics 101: Credible vs Confidence Interval [https://towardsdatascience.com/statistics-101-credible-vs-confidence-interval-af7b7e8fdd79/]
• 40. What's the difference between a confidence interval and a ... [https://stats.stackexchange.com/questions/2272/whats-the-difference-between-a-confidence-interval-and-a-credible-interval]
• 41. Expert agreement in prior elicitation and its effects on ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9568464/]
• 42. Refined modeling of sensor reliability in the belief function ... [https://www.sciencedirect.com/science/article/abs/pii/S1566253506000698]
• 43. Addressing prior dependence in hierarchical Bayesian ... [https://arxiv.org/html/2511.03667v1]
• 44. Bayesian Network in Structural Health Monitoring [https://pmc.ncbi.nlm.nih.gov/articles/PMC12196708/]
• 45. Application of Bayesian networks in reliability assessment [https://www.sciencedirect.com/science/article/abs/pii/S2352012424022525]
• 46. Reliability Analysis of CVT Online Monitoring Device ... [https://www.mdpi.com/1996-1073/18/18/4928]
• 47. A general framework of Bayesian network for system ... [https://www.sciencedirect.com/science/article/abs/pii/S0951832021004658]
• 48. Bayesian network approach for reliability analysis of ... [https://www.nature.com/articles/s41598-024-52694-0]
• 49. Modeling of Complex Redundancy in Technical Systems ... [https://papers.phmsociety.org/index.php/phme/article/view/1580]
• 50. Validity and reliability of accelerations and orientations ... [https://www.nature.com/articles/s41598-022-18845-x]
• 51. On the Reliability of Wearable Technology [https://pmc.ncbi.nlm.nih.gov/articles/PMC10346338/]
• 52. Improving the reliability of the frequency response function ... [https://www.sciencedirect.com/science/article/abs/pii/S1270963816301316]
• 53. A comprehensive Bayesian approach for model updating ... [https://www.sciencedirect.com/science/article/abs/pii/S0266892011000439]
• 54. Bayesian Architecture for Predictive Monitoring of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11679446/]
• 55. On the hierarchical Bayesian modelling of frequency ... [https://www.sciencedirect.com/science/article/pii/S0888327023009809]
• 56. On the hierarchical Bayesian modelling of frequency ... [https://arxiv.org/html/2307.06263v2]
• 57. Analytical hierarchical Bayesian modeling framework for ... [https://www.sciencedirect.com/science/article/abs/pii/S0045782525006139]
• 58. Improved Bayesian Model Updating Method for Frequency ... [https://www.mdpi.com/2227-7390/12/13/2076]
• 59. An Optimal Sensor Layout Using the Frequency Response ... [https://www.mdpi.com/1424-8220/22/10/3778]
• 60. Bayesian reliability demonstration for failure-free periods [https://www.sciencedirect.com/science/article/abs/pii/S0951832004001474]
• 61. Reliability evaluation of optoelectrical attitude sensors for ... [https://www.sciencedirect.com/science/article/abs/pii/S0263224125022183]
• 62. A Bayesian Approach to Research [https://oit.utk.edu/news/bayesian-approach-to-research/]
• 63. Bayesian networks supporting management practices [https://www.sciencedirect.com/science/article/pii/S266709682400020X]
• 64. Advances in approximate Bayesian inference for models in ... [https://www.sciencedirect.com/science/article/pii/S175543652500043X]
• 65. Efficient variational Bayesian model updating by ... [https://www.sciencedirect.com/science/article/abs/pii/S0888327024010112]
• 66. The rise and fall of Bayesian statistics [https://statmodeling.stat.columbia.edu/2025/08/10/the-rise-and-fall-of-bayesian-statistics/]
• 67. Model selection for degradation-based Bayesian reliability ... [https://www.sciencedirect.com/science/article/abs/pii/S0278612515000734]
• 68. BAYESIAN HIERARCHICAL MODELING AND ANALYSIS ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10815935/]
• 69. RELIABILITY ANALYSIS FOR SENSOR NETWORKS AND ... [https://www.cambridge.org/core/journals/proceedings-of-the-design-society/article/reliability-analysis-for-sensor-networks-and-their-data-acquisition-a-systematic-literature-review/81EC3EB8B0C11727389ED7E4BF98C510]
• 70. Physics of failure [https://en.wikipedia.org/wiki/Physics_of_failure]
• 71. What Is Physics of Failure? [https://www.ansys.com/blog/what-is-physics-of-failure]
• 72. Reliability Assessment Using Physics-of-Failure Principles ... [https://sma.nasa.gov/news/articles/newsitem/2017/05/22/reliability-assessment-using-physics-of-failure-principles-modeling-and-simulation]
• 73. Reliability Engineering Terms – Physics of Failure (PoF) [https://www.quanterion.com/terms-physics-of-failure-pof/?srsltid=AfmBOoqpi_8k5KtZOYggiLIRDwC8pjix8vO_Jt_EKnLNoSqDuN_fkRQd]
• 74. A Bayesian-network-based quantum procedure for failure risk ... [https://epjquantumtechnology.springeropen.com/articles/10.1140/epjqt/s40507-023-00171-4]
• 75. Bayesian networks in reliability [https://www.cee.ed.tum.de/era/research/completed-research-projects/bayesian-networks-in-reliability/]
• 76. A Physics-of-Failure (PoF) model-based Dynamic ... [https://www.sciencedirect.com/science/article/pii/S0950423024001608]
• 77. A Physics-of-Failure (Pof) Model-Based Dynamic Bayesian ... [https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4777435]
• 78. Classical versus Bayesian risks in acceptance sampling [https://link.springer.com/content/pdf/10.1007/s00180-012-0360-y.pdf?pdf=button]
• 79. Classical Versus Bayesian Error-Controlled Sampling ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12110634/]
• 80. Risk-embedded Bayesian acceptance sampling plans via ... [https://www.sciencedirect.com/science/article/abs/pii/S0360835213001411]
• 81. An optimal sensor design framework accounting for ... [https://www.sciencedirect.com/science/article/abs/pii/S0888327023005812]
• 82. Bayesian and Classical Machine Learning Methods [https://www.mdpi.com/2072-4292/10/1/39]
• 83. Data Reliability in 2025: Definition, Examples & Tools [https://atlan.com/what-is-data-reliability/]
• 84. Understanding Success Criterion 1.4.3: Contrast (Minimum) [https://www.w3.org/WAI/WCAG21/Understanding/contrast-minimum.html]
• 85. Sensor Informativeness, Identifiability, and Uncertainty in ... [https://arxiv.org/html/2511.16628v1]
• 86. Uncertainty-aware power consumption prediction in ... [https://www.sciencedirect.com/science/article/pii/S0278612525002560]
• 87. Uncertainty Guided Online Ensemble for Non-stationary ... [https://arxiv.org/html/2511.02092v1]
• 88. Sensor Market 2025-2035: Technologies, Trends, Players, ... [https://www.idtechex.com/en/research-report/sensor-market/1038]
• 89. Sensors in 2025: Global Market Trend Report [https://www.azosensors.com/article.aspx?ArticleID=3258]
• 90. The Validation and Accuracy of Wearable Heart Rate Trackers ... [https://formative.jmir.org/2025/1/e70835]
• 91. Wearable Devices in Healthcare Beyond the One-Size-Fits All ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12568095/]
• 92. Evaluation of the Validity and Reliability of NeuroSkin's ... [https://pubmed.ncbi.nlm.nih.gov/41007205/]
• 93. Why Brain Wearables Are Making Traditional EEG Labs ... [https://globalrph.com/2025/10/why-brain-wearables-are-making-traditional-eeg-labs-obsolete-in-2025/]
• 94. Comparing the Accuracy of Different Wearable Activity ... [https://www.researchprotocols.org/2025/1/e70472]
• 95. A Framework for Evaluating the Reliability of Health ... [https://www.mdpi.com/2078-2489/16/10/833]
• 96. Understanding Bayesian analysis of clinical trials [https://pmc.ncbi.nlm.nih.gov/articles/PMC12094692/]
• 97. Credible Intervals (CI) • bayestestR - easystats [https://easystats.github.io/bayestestR/articles/credible_interval.html]
• 98. Credible interval [https://en.wikipedia.org/wiki/Credible_interval]
• 99. Excessive precision compromises accuracy even with ... [https://www.nature.com/articles/s41534-025-01071-4]